PHY.K02 Molecular and Solid State Physics
29.01.2021

Name   Matrikelnr.

(This was an online exam. The students had access to the internet.)

Problem 1

The 1s orbital for hydrogen is,

$$\phi_{\text{1s}}=\frac{1}{\sqrt{\pi a_0^3}}\exp\left(-\frac{r}{a_0}\right)$$

What is the electron probability density of the 1s orbital of hydrogen at $r=$ $a_0$? The Bohr radius is $a_0 = 5.2917721\times 10^{-11}$ m.

1/m³

What is the many electron Hamitonian of ?

                                            

The many electron wave function for is defined in a space of more than three dimensions. How many dimensions does this wave function have?

dimensions

The wavefunction for is,

  1. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow \rangle$
  2. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow \rangle$
  3. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow \rangle$
  4. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow ,\phi_{\text{2p}_x}\uparrow \rangle$
  5. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow ,\phi_{\text{2p}_x}\uparrow ,\phi_{\text{2p}_x}\downarrow \rangle$
  6. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow ,\phi_{\text{2p}_x}\uparrow ,\phi_{\text{2p}_x}\downarrow ,\phi_{\text{2p}_y}\uparrow \rangle$
  7. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow ,\phi_{\text{2p}_x}\uparrow ,\phi_{\text{2p}_x}\downarrow ,\phi_{\text{2p}_y}\uparrow ,\phi_{\text{2p}_y}\downarrow \rangle$
  8. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow ,\phi_{\text{2p}_x}\uparrow ,\phi_{\text{2p}_x}\downarrow ,\phi_{\text{2p}_y}\uparrow ,\phi_{\text{2p}_y}\downarrow ,\phi_{\text{2p}_z}\uparrow \rangle$
  9. $|\phi_{\text{1s}}\uparrow ,\phi_{\text{1s}}\downarrow ,\phi_{\text{2s}}\uparrow ,\phi_{\text{2s}}\downarrow ,\phi_{\text{2p}_x}\uparrow ,\phi_{\text{2p}_x}\downarrow ,\phi_{\text{2p}_y}\uparrow ,\phi_{\text{2p}_y}\downarrow ,\phi_{\text{2p}_z}\uparrow ,\phi_{\text{2p}_z}\downarrow \rangle$

The wave function above is not the true many-electron wave function. Explain what approximations have to be made to write the wave function like this.

Slater introduced effective nuclear charges. What happens to the size and the shape of the wave functions when the effective nuclear charge changes?

Problem 2

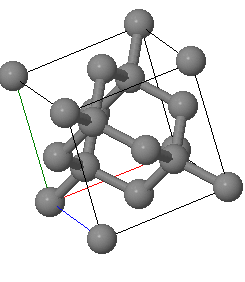
X-rays with an wavelength of 0. Å are used to analyze a crystal with a diamond crystal structure with a lattice constant of  Å.

The diffraction peaks are labeled using the conventional (cubic) unit cell. If the primary beam is directed in the positve $x$-direction, what are $\vec{k}$, $\vec{k}'$ and $\vec{G}$ for the reflection?

$\vec{k}=$ $\hat{k}_x +$ $\hat{k}_y +$ $\hat{k}_z $ 1/m

$\vec{G}$ = $\hat{k}_x +$ $\hat{k}_y +$ $\hat{k}_z $ 1/m

$\vec{k}'=$ $\hat{k}_x +$ $\hat{k}_y +$ $\hat{k}_z $ 1/m

Problem 3

A metal has an fcc crystal structure with one atom in the basis. The lattice constant is . Å and this metal has one valence electron.

Estimate the phonon contribution to the specific heat at 800° C.

$c_v$ (phonon) = J/(K m³).

Use the free electron model to estimate the electron contribution to the specific heat at 800° C.

$c_v$ (electron) = J/(K m³).

What is the Fermi wave number in the free electron model?

$k_F = $ 1/m.

How far is the closest point on the first Brillouin zone boundary to the origin in reciprocal space?

$k = $ 1/m.

A semiconductor has a Zincblende (fcc) crystal structure with two atoms in the basis. The lattice constant is . Å and the band gap is 1. eV. The zero of energy is taken to be the top of the valence band $E_v = 0$.

What is the chemical potential of this semiconductor?

$\mu =$ eV.

The semiconductor and the metal have the same lattice constant. Which has a higher specific heat? Explain your reasoning.

Problem 4

Neutral atoms A and B are far apart from each other. This situation is assigned an energy $E=0$. An electron is taken from atom A and put to atom B. This increases the energy by the ionization energy of atom A, . eV, minus the electron affinity of atom B, 2 eV. The ions are then slowly brought together and as they get closer, the energy of the system decreases like a Coulomb potential. At which distance is the energy zero again?

$d =$ m.

Explain what the Madelung constant is.

The cohesive energy of an ionic crystal can be described by the function,

$$U_{tot}= N\left(z\lambda e^{-R/\rho}-\frac{\alpha e^2}{4\pi\epsilon_0 R}\right).$$

Here $N$ is the number of primitive unit cells in the crystal, $R$ is the interatomic spacing, $z$ is the number of nearest neighbors, $\lambda,\rho$ and $\alpha$ are constants. An ionic crystal is put inside a pressure cell in an x-ray diffractometer. Explain how you can measure $\rho$ and $\lambda$. Assume that $\alpha$ and $z$ are known.

The CsCl structure has the largest Madelung constant and therefore ionic crystals forming this structure have the lowest energy. Explain why some ionic crystals form the NaCl or Zincblend crystal structures instead of the low energy CsCl structure.