Name Matrikelnr.
(This was an online exam. The students had access to the internet.)
Van der Waals bonds are often described by a Lennard-Jones potential with the form, $U(R)= 4\epsilon\left[\left(\frac{\sigma}{R}\right)^{12}-\left(\frac{\sigma}{R}\right)^{6}\right]$, where $\epsilon=$ meV and $\sigma=$ Å are characteristic constants for the bond and $R$ is the bond length (the distance between the atoms).
X-rays with an wavelength of 0. Å are used to analyze a crystal with a sodium chloride crystal structure with a lattice constant of Å.

The diffraction peaks are labeled using the conventional (cubic) unit cell. If the primary beam is directed in the positve $x$-direction, what are $\vec{k}$, $\vec{k}'$ and $\vec{G}$ for the reflection?
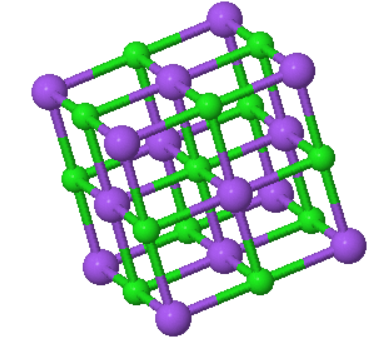
A conventional unit cell of NaCl is shown below. The Bravais lattice is fcc. The lattice contants are given in the figure.

(a) A crystal of NaCl is mm × mm × mm. How many $k$ states are there in the first Brillouin zone?