(a) What is the molecular orbital Hamiltonian that needs to be solved?

(b) Write down the many-electron wavefunction in terms of the solutions of the molecular orbital Hamiltonian.

(c) How would the many-electron wavefunction be used to calculate the bond potential?

(d) Once a bond potential has been calculated, it is often fit to a Morse potential of the form,

For N₂, the results are: $U_0 = 9.77$ eV, $r_0=1.08$ Å, a=2.73Å^-1. The mass of a nitrogen atom is 14 amu. 1 amu = $1.66\times 10^{-27}$ kg.

What are the vibrational and rotational frequencies of N₂?

Problem 2

In a diffraction experiment on a single crystal, the incoming x-rays have a wave vector $\vec{k} = 10^{10} \hat{x}$ 1/m and diffraction peaks are measured at

$\vec{k}' = 1.1\times 10^{10} \hat{x}$
$\vec{k}' = 0.9\times 10^{10} \hat{x}$
$\vec{k}' = 10^{10} \hat{x} + 10^9 \hat{y}$
$\vec{k}' = 10^{10} \hat{x} - 10^9 \hat{y}$
$\vec{k}' = 10^{10} \hat{x} + 10^9 \hat{z}$
$\vec{k}' = 10^{10} \hat{x} - 10^9 \hat{z}$

(a) What are the primitive lattice vectors in real space $(\vec{a}_1,\,\vec{a}_2,\,\vec{a}_3)$ for this crystal?

(b) What is the magnitude of the largest reciprocal lattice vector $|\vec{G}|$ that could be measured in this experiment?

(c) What additional information would you need to determine how the atoms are arranged in the primitive unit cell?

(d) If the crystal was ground up into a powder, at what angle $2\theta$ would a diffraction peak be measured in powder diffraction?

Problem 3

This question is about calculating the phonon dispersion relation.

(a) The atomic vibrations are modeled as a coupled mass-spring system. How do we know which masses to use and how do we know what spring constants to use?

(b) The mass-spring system is described by coupled differential equations. As long as the springs are linear, the form of the solution to these equations is known. What do you know about these solutions? Give the form of the solutions if possible.

(c) How many $k$-values are there in the first Brillouin zone?

(d) How does the number of branches in the phonon dispersion relation depend on the number of atoms in the primitive unit cell?

(e) Describe how the phonon density of states is calculated.

Problem 4

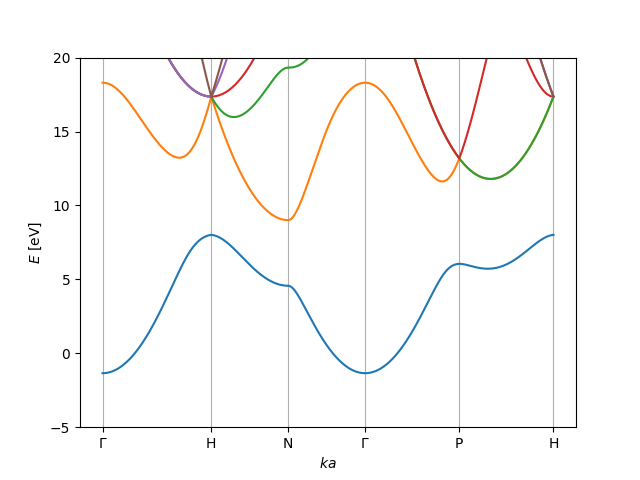
(a) To the right is a band structure. There are 3 electrons per unit cell for the bands that are drawn. Draw the chemical potential into the band diagram and state if this material is a metal, a semiconductor, or an insulator.

(b) The electron wavefunctions in a crystal have Bloch form, $\psi = e^{i\vec{k}\cdot\vec{r}}u_{\vec{k}}(\vec{r})$. What values can $\vec{k}$ have? What property does $u_{\vec{k}}(\vec{r})$ have?

(c) In the tight-binding method you guess a form for the wavefunction and then calculate the energy by substituting this wavefunction into the Schrödinger equation. What is the tight-binding wavefunction that is guessed?

(d) Why are only the electron states near the Fermi surface responsible for the electronic contribution to the thermodynamic properties of a metal?