Name Matrikelnr.
Each subsections (a), (b), (c), $\cdots$ can be awarded a maximum of 3 points.
Problem 1 Consider a LiF molecule. Lithium has 3 protons and flourine has 9 protons. (a) What kind of bond do you expect in a LiF molecule? Explain your reasoning. (b) If the a trial wavefunction consists of the 1s and 2s orbitals of lithium and the 1s, 2s, and 2p orbitals of flourine, how many molecular orbitals will be calculated? (c) How many of the molecular orbitals calculated in (b) will be occupied in the ground state of LiF? (d) Is the spacing between the rotational levels larger for LiF or HF? Explain your reasoning. (e) Describe an experiment that could be used to determine the effective spring constant of the LiF bond. Problem 2
 |
The element Sn is a metal above 13° C and a semiconductor below 13° C.
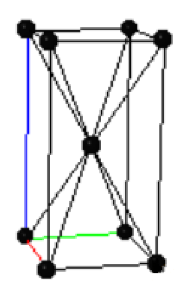
(a) The metallic phase has a body centered tetragonal Bravais lattice with two atoms in the primitive unit cell. The conventional unit cell of the metallic phase is shown on the right where the black points are the Bravais lattice points. How many atoms are there in the conventional unit cell? Explain your reasoning.
(b) The semiconducting phase has an fcc Bravais lattice with two atoms in the primitive unit cell. The conventional lattice constant is 6.489 Å. What is the volume of the primitive unit cell?
(c) The semiconducting phase has a very small direct band gap at $\Gamma$. Draw the electron dispersion relation $E\text{ vs. }k$ for the semiconducting phase showing the valence band, the conduction band and the chemical potential.
(d) Which has more phonon modes, 10 grams of the metallic phase or 10 grams of the semiconducting phase? Explain your reasoning.
(e) Which has a higher specific heat at room temperature, the metallic phase or the semiconducting phase? Explain your reasoning.
Problem 3
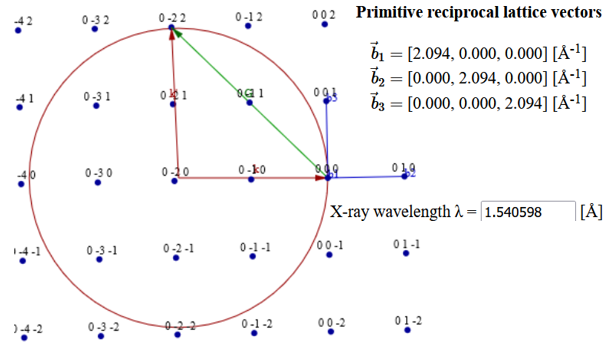
(a) A cross section of the Ewald sphere is shown below. What is the diffraction angle $2\theta$ for the Green reciprocal lattice vector?
(b) You are given a crystal of some unknown material and are asked to determine the crystal structure using x-ray diffraction. Explain how you can measure the reciprocal lattice vectors in an x-ray diffraction experiment.
(c) Explain how you can determine the primitive reciprocal lattice vectors from the measured reciprocal lattice vectors.
(d) Explain how you can determine the real space primitive lattice vectors from the primitive reciprocal lattice vectors.
Problem 4
(a) Quartz is a transparent crystal that is often found in the mountains. Quartz makes a structural phase transition from α-quartz to β-quartz at a high temperature. How would you calculate the temperature at which this transition takes place? Your answer should discuss the electron contribution and the phonon contribution.
(b) What can you deduce about the electronic bandstructure of quartz from knowing it is transparent?
(c) A metal is well described by the free electron model with an effective mass equal to the free electron mass. The chemical potential is 1 eV above the bottom of the band. What is the Fermi wave vector $k_F$ of this metal? Some constants are given under problem 4.
(d) If the metal described by a free electron model is compressed, will the chemical potential increase, decrease, or stay the same? Explain your reasoning.