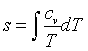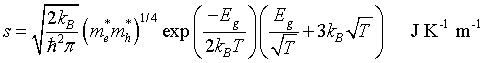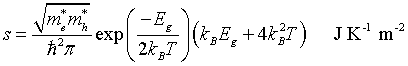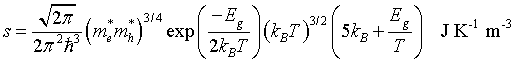Boltzmann approximation

The table below gives the contribution of electrons in intrinsic semiconductors and insulators to some thermodynamic quantities. These results where calculated in the Boltzmann approximation where it is assumed that the chemical potential lies in the band gap more than 3k_BT from the band edge. The electronic contribution to the thermodynamic quantities are usually much smaller than the contribution of the phonons and thus the electronic components are often simply ignored.

	1-d	2-d	3-d
Density of states	$D(E) = \begin{cases} \frac{D_v}{\sqrt{E_v-E}}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ \frac{D_c}{\sqrt{E-E_c}}, & \mbox{for } E_c \lt E \end{cases}$	$D(E) = \begin{cases} D_v, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ D_c, & \mbox{for } E_c \lt E \end{cases}$	$D(E) = \begin{cases} D_v\sqrt{E_v-E}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ D_c\sqrt{E-E_c}, & \mbox{for } E_c \lt E \end{cases}$
Density of states $m_e^$ and $m_h^$ are 'density of states' effective masses	$D(E) = \begin{cases} \frac{1}{\hbar\pi}\sqrt{\frac{2m^_h}{E_v-E}}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ \frac{1}{\hbar\pi}\sqrt{\frac{2m^_e}{E-E_c}}, & \mbox{for } E_c \lt E \end{cases}$	$D(E) = \begin{cases} \frac{m_h^}{\hbar^2\pi}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ \frac{m_e^}{\hbar^2\pi}, & \mbox{for } E_c \lt E \end{cases}$	$D(E) = \begin{cases} \frac{(2m_h^)^{\frac{3}{2}}}{2\pi^2\hbar^3}\sqrt{E_v-E}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ \frac{(2m_e^)^{\frac{3}{2}}}{2\pi^2\hbar^3}\sqrt{E-E_c}, & \mbox{for } E_c \lt E \end{cases}$
Density of states $N_v$ and $N_c$ are effective densities of states	$D(E) = \begin{cases} N_v(300)\sqrt{\frac{2}{300\pi k_B(E_v-E)}}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ N_c(300)\sqrt{\frac{2}{300\pi k_B(E-E_c)}}, & \mbox{for } E_c \lt E \end{cases}$	$D(E) = \begin{cases} \frac{N_v(300)}{300k_B}H(E_v-E), & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ \frac{N_c(300)}{300k_B}H(E-E_c), & \mbox{for } E_c \lt E \end{cases}$	$D(E) = \begin{cases} \frac{2N_v(300)}{\sqrt{\pi}}\left(\frac{1}{300k_B}\right)^{\frac{3}{2}}\sqrt{E_v-E}, & \mbox{for } E\lt E_v \\ 0, & \mbox{for } E_v\lt E\lt E_c \\ \frac{2N_c(300)}{\sqrt{\pi}}\left(\frac{1}{300k_B}\right)^{\frac{3}{2}}\sqrt{E-E_c}, & \mbox{for } E_c \lt E \end{cases}$
Density of electrons in the conduction band $n=\int\limits_{E_c}^{\infty}D(E)f(E)dE$	$n=\sqrt{\frac{m_e^*k_BT}{\hbar^2\pi}}\exp\left(\frac{\mu-E_c}{k_BT}\right)\quad\text{m}^{-1}$ $=N_c(T)\exp\left(\frac{\mu-E_c}{k_BT}\right)$
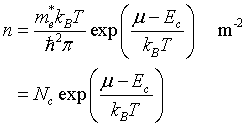
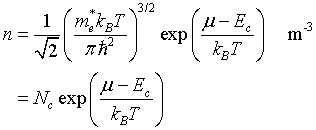
Density of electrons in the conduction band $n=\int\limits_{E_c}^{\infty}D(E)f(E)dE$
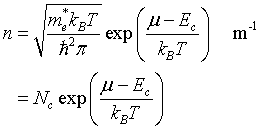
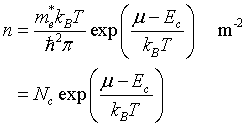
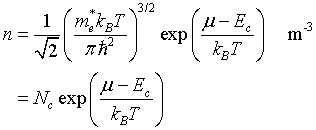
Density of holes in the valence band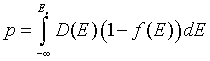
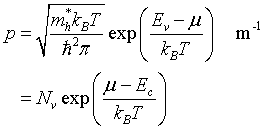
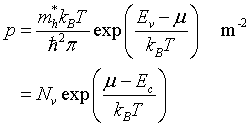
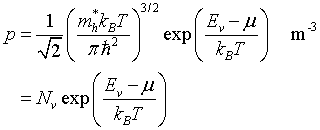
Law of mass action
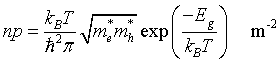
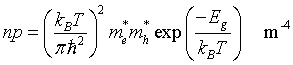
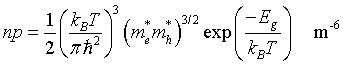
Intrisic carrier density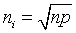
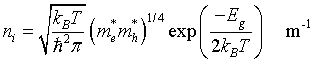
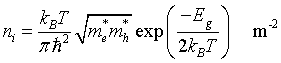
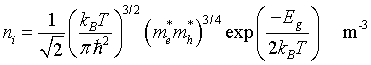
Chemical potential Set n = p, solve for μ
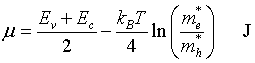
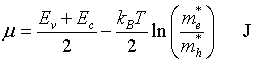
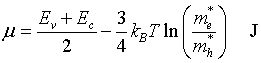
Internal energy density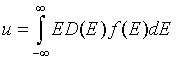
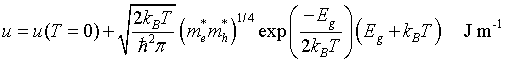
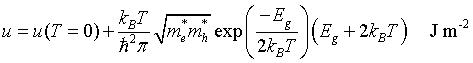
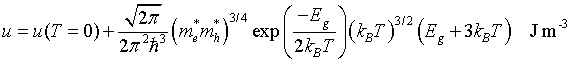
Helmholtz free energy f = u - Ts
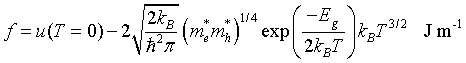
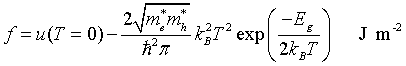
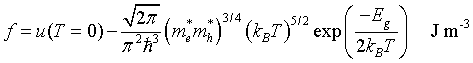
Specific heat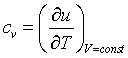
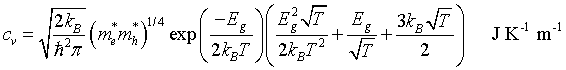
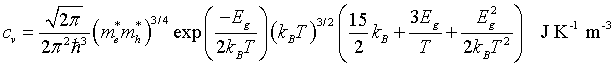
Entropy

The mathematical functions that can be used are list below. Multiplication must be specified with a '*' symbol, 3*cos(x) not 3cos(x). Powers are specified with the 'pow' function: x³ is pow(x,3) or x**3 not x^3.
<table align='center'><tr><td><ul><li>abs(x) - absolute value</li><li>acos(x) - inverse cosine</li><li>acosh(x) - inverse hyperbolic cosine</li>
<li>asin(x) - inverse sine</li><li>asinh(x) - inverse hyperbolic sine</li><li>atan(x) - inverse tangent</li><li>atanh(x) - inverse hyperbolic tangent</li><li>cos(x) - cosine</li><li>cosh(x) - hyperbolic cosine</li>
<li>exp(x) - et</li></ul></td>
<td><ul><li>log(x) - natural logarithm</li><li>pi = 3.141592653589793</li><li>pow(t,y) - compute ty</li><li>round(x) - round to the nearest integer</li>
<li>sin(x) - sine</li><li>sinh(x) - hyperbolic sine</li><li>sqrt(x) - square root</li><li>tan(x) - tangent</li><li>tanh(x) - hyperbolic tangent</li><li>H(x) - Heaviside function = 0 for x < 0, 1 for x > 0</li></ul></td></tr></table>
 
<a href="https://lampz.tugraz.at/~hadley/physikm/script/intro/vectorscript.en.php?print">Vector functions</a> 
<table align='center'><tr><td><ul><li>cross(A,B) - cross product</li><li>dot(A,B) - scalar product of two vectors </li><li>dot(a,B) - scalar a times vector B</li><li>length(A) - length of a vector</li></ul></td><td valign="top"><ul><li>unit(A) - unit vector in direction of A</li><li>vadd(A,B) - vector addition A + B</li><li>vsub(A,B) - vector subtraction A -B</li></ul></td></tr></table>

● print(x) - Text or variables can be printed to the Script Output box with the print(x) function. Text should be put in quotes, print("Print some text"). The value of variable x can be printed with print(x) and text can be mixed with variables by concatenating them together with a + sign, print("The length is "+x+" m.").

//For Silicon kB = 1.380649E-23; // [J/K] Boltzmann's constant hbar = 1.054571817E-34; // [J s] reduced Planck's constant e = 1.602176634E-19; // [C] elementary charge pi = 3.141592653589793; Dc = 6.874E21; // [eV^(-3/2) cm^(-3)] Constant describing the density of states at the conduction band edge Dv = 3.8775E21; // [eV^(-3/2) cm^(-3)] Constant describing the density of states at the valence band edge DcSI = Dcpow(e,-3/2)1E6; //[J^(-1) m^(-3)] DvSI = Dvpow(e,-3/2)1E6; //[J^(-1) m^(-3)] mh = 0.5pow(2pipihbarhbarhbarDvSI,2/3); // [kg] density of states effective hole mass me = 0.5pow(2pipihbarhbarhbarDcSI,2/3); // [kg] density of states effective electron mass Nc300 = (2Dc/sqrt(pi))pow(kB300/e,3/2); // Effective density of states of the conduction band at 300 K Nv300 = (2Dv/sqrt(pi))pow(kB300/e,3/2); // Effective density of states of the valence band at 300 K T = 300; // temperature [K] Eg = 1.166-4.73E-4TT/(T+636); //[eV] mu = Eg/2 + kBTlog(Dv/Dc)/e; // [eV] chemical potential ni = sqrt(0.25piDcDvpow(kBT/e,3)exp(-eEg/(kBT))); // [1/cm^3] intrinsic carrier concentration ni=n=p u = (sqrt(2pi)/(2pipihbarhbarhbar))pow(memh,3/4)exp(-eEg/(2kBT))pow(kBT,3/2)(eEg + 3kBT); // [J/m^3] internal energy density f = -(sqrt(2pi)/(pipihbarhbarhbar))pow(memh,3/4)exp(-eEg/(2kBT))pow(kB*T,5/2); // [J/m^3] Helmholtz free energy density
Script Output