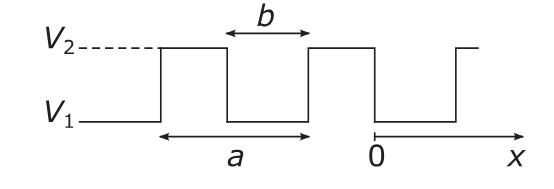
Consider an electron confined to a potential of the form,
$$V(f_{\text{square}}(x) + f_{\text{square}}(y) + f_{\text{square}}(z)),$$where $V = V_2 - V_1$ is the amplitude of the potential and $f_{\text{square}}(x)$ is a square wave function.

This potential has the advantage that the density of states can be easily calculated for a given set of parameters $V$ and $b/a$. [1]
The thermodynamic properties depend dramatically on the number of electrons per primitive unit cell $n$. For the same dispersion relation and density of states, the crystal can be a metal, a semiconductor, or an insulator depending on the number of electrons per primitive unit cell.
|
| |
|
| |
|
|