Problem 1
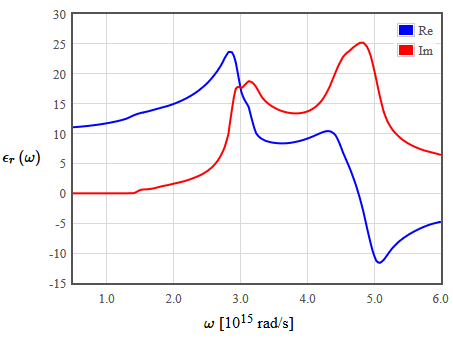
The dielectric function of some material is shown in the folowing figure.

(a) What properties does this material have? Note that the real part of the dielectric function is negative for some frequencies.

(b) What are the limiting values of the real and imaginary parts of the dielectric function at $\omega=0$ and $\omega\rightarrow\infty$?

(c) How is the dielectric function related to optical absorption measurements?

(d) How is the dielectric function related to conductivity measurements at microwave frequencies?

Problem 2
(a) How can the Fermi surface be calculated theoretically?

(b) How can the Fermi surface be measured?

(c) Why are the states near the Fermi surface the most important for the electrical contribution to the specific heat and the thermal conductivity?

(d) What are electron-like orbits and hole-like orbits at the Fermi surface. How could you observed them experimentally?

Problem 3

(a) In the Nerst effect, a sample is placed in a magnetic field and a temperature gradient that are perpendicular to each other. The electric field in the direction perpendicular to both the magnetic field and the temperature gradient is measured. How could the Boltzmann equation be used to calculate this electric field?

(b) How does the Nerst effect depend on the electron and phonon dispersion relations?

(c) What is the relaxation time approximation? What changes in a relaxation time?

Problem 4
Barium titanate is a ferroelectric that undergoes a first order structural phase transition from a rhombohedral phase to a monoclinic phase at about -80 C.

(a) What could be used as the order parameter? What symmetry is broken?

(b) Explain briefly what the Landau theory of first order phase transitions is.

(c) Sketch the specific heat and the electric susceptibility of barium titanate as a function of temperature. Where does the latent heat appear in these plots?

(d) Sketch the pyroelectric coefficient as a function of temperature for barium titanate.