Problem 1
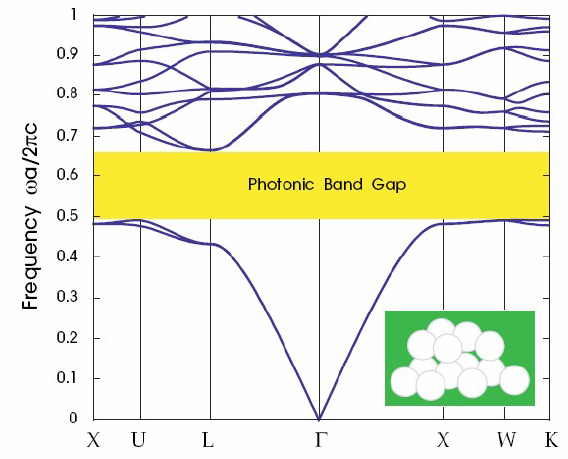
The photon dispersion relation of a photonic crystal is shown in the image below. The structure consists of empty holes on a diamond lattice etched in a material with a dielectric constant of $\epsilon_r=13$.

Source: http://ab-initio.mit.edu/book/

(a) Sketch the dielectric function as a function of frequency for this material.

(b) Describe how the periodic structure of the photonic crystal would effect the phonon dispersion of this material.

(c) What would you expect to measure with Raman spectroscopy on this material?

Problem 2

How could you determine the Fermi surface of magnesium theoretically?

How could you determine the Fermi surface of magnesium experimentally?

How could use a description of the Fermi surface to calculate the electronic contribution to the specific heat of magnesium?

How could use a description of the Fermi surface to calculate the electrical conductivity of magnesium?

Problem 3
By shining light on a semiconductor, excitons are created.

(a) Describe what an exciton is.

(b) By adjusting the intensity of the light, the density of excitons can be controlled. At high exciton densities, the semiconductor goes through a Mott transition. Explain what this means.

(c) By changing the light intensity at the frequency that creates excitons, it would be possible to adjust the plasma frequency. Explain why the plasma frequency would change. What properties of the material would be modulated by changing the plasma frequency?

Problem 4
(a) Explain how the exchange energy leads to ferromagnetism.

(b) What is mean field theory? How is mean field theory used to calculate the Curie-Weiss law?

(c) How was Landau's theory of phase transitions used to calculate the Curie-Weiss law?