1. Electron-electron Interactions

1. Explain why electron-electron interactions are difficult to describe.
2. Because of the mathematical difficulties of solving the Schrödinger equation including the electron-electron interactions, we often consider systems of non-interacting electrons. Landau's theory of a Fermi liquid shows that we should really consider non-interacting quasipartcles instead of non-interacting electrons. Describe these non-interacting quasiparticles. What properties do they have?
3. A simple model for electron-electron interactions is electron screening. Explain what screening is and how it can be used to explain a Mott transition.
4. Single electron effects are another simple way to include electron-electron interactions. Explain the single-electron charging effect.
5. How can the density of excitons be related to a metal-insulator transition?

Solution

1. Explain why electron-electron interactions are difficult to describe.

   The full non-relativistic Hamiltonian of a solid is

   \begin{equation*} H = -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}+\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} \end{equation*}

   and usually the nuclei are considered fixed (Born-Oppenheimer approximation), leading to

   \begin{equation*} H = -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|} \end{equation*}

   However, the exact wave function solving the corresponding Schrödinger equation is still a function of the positions of all electrons in the crystal. Storing it in a computer on a grid with $M$ points per dimension would thus require storing $M^{3N}$ complex numbers. In a macroscopic crystal of 1 cm³ there are about 10²⁴ atoms with many electrons each, which makes this exact wave function impossible to handle.

   Therefore, for many applications the electron-electron interactions are neglected as a first approximation. Then methods like tight binding or the plane wave method can be applied.

2. Because of the mathematical difficulties of solving the Schrödinger equation including the electron-electron interactions, we often consider systems of non-interacting electrons. Landau's theory of a Fermi liquid shows that we should really consider non-interacting quasipartcles instead of non-interacting electrons. Describe these non-interacting quasiparticles. What properties do they have?

   See question 1 in Quasiparticles.

3. A simple model for electron-electron interactions is electron screening. Explain what screening is and how it can be used to explain a Mott transition.

   In this model the interaction of the electrons is taken into account by modifying the potential of the nuclei - we can imagine that the negative charge of the other electrons screens the positive charge of the nucleus for one particular electron, which "sees" only a reduced charge.

   Screening is an electrostatic phenomenon and can therefore be described with the Poisson equation, which for the potential of a single nucleus at $\vec{r} = 0$ reads

   \begin{equation*} \nabla^{2} \phi = \frac{Ze \delta(\vec{r})}{\epsilon_{0}} \end{equation*}

   and has the well-known solution

   \begin{equation*} \phi(\vec{r}) = \frac{Ze}{4\pi\epsilon_0|\vec{r}|}. \end{equation*}

   In the presence of electrons the potential $\phi$ will be modified by their charge density around the nucleus,

   \begin{equation*} \nabla^{2} \phi = \frac{Ze \delta(\vec{r})}{\epsilon_{0}} - \frac{\rho_{ind}(\vec{r})}{\epsilon_{0}}. \end{equation*}

   For a non-interacting electron gas it turns out that the induced charge is proportional to the potential (Thomas-Fermi approximation):

   \begin{equation*} \rho_{ind}(\vec{r}) = -\epsilon_0k_s^2\phi(\vec{r}). \end{equation*}

   Inserting this expression into the Poisson equation yields the Helmholtz equation

   \begin{equation*} \nabla^{2} \phi - k_s^2\phi = \frac{Ze \delta(\vec{r})}{\epsilon_{0}} \end{equation*}

   with the solution

   \begin{equation*} \phi(\vec{r}) = \frac{Ze}{4\pi\epsilon_0|\vec{r}|}e^{-k_s|\vec{r}|}. \end{equation*}

   Thus, the potential of the ion is exponentially screened compared to the potential without other electrons.

   

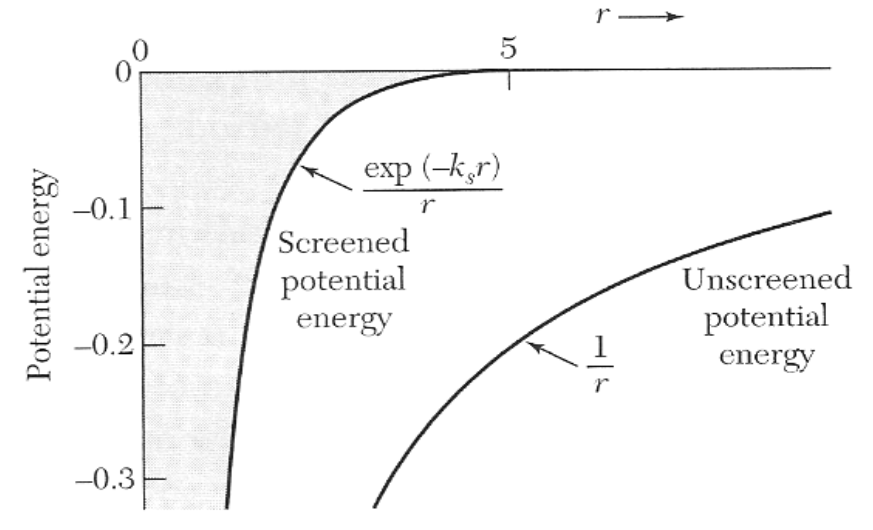   Figure 1: Unscreened and screened Coulomb potential.

   The consequences of this effect can be understood by considering a potential well of finite width. Inside such a potential there is a finite number of allowed states and this number decreases when the width becomes smaller.

   If the atoms are far apart from each other, such that the orbitals do not overlap, all electrons are bound in the potential of their respective atom. When the atoms are brought closer together, at some point the orbitals start to overlap and the screening effect described above starts. This makes the potential narrower (see figure above) and thus the number of available bound states decreases. Eventually the highest occupied electron state will "pop out" of the potential well and become an unbound state, leaving the material in a metallic state with moving electrons. This transition occurs at a sharp value of the screening wave vector $k_s$ and is called Mott transition.

   The critical screening wave vector can be obtained by solving the Schrödinger equation for the screened potential. For hydrogen atoms it turns out that the 1s state becomes unbound at

   \begin{equation*} k_s < 1.19/a_0, \end{equation*}

   where $a_0$ is the Bohr radius and from that follows the Mott criterion

   \begin{equation*} n^{-1/3} \leq Ca_0^{*}. \end{equation*}

   Here $n$ is the electron density, $C$ is a constant (between 2.5 and 4) and $a_0^{*}$ is the effective Bohr radius.

4. Single electron effects are another simple way to include electron-electron interactions. Explain the single-electron charging effect.

   The single-electron charging effect occurs in small structures, such as quantum dots, which are connected to leads via tunnel junctions (i.e. thin layers of dielectrics where electrons can tunnel to and from the quantum dot). These junctions form capacitors and due to the small size of the quantum dot, their capacitance is very small (∼10^-18 F).

   Now consider a bias voltage applied to the leads. Putting an additional electron on the quantum dot costs an energy $e^2/2C$ and if the voltage is small, the electrons in the leads do not have enough energy to overcome that energy barrier. This is called the Coulomb blockade. Because of the tiny capacitance $C$ the Coulomb blockade can persist up to rather high voltages in the range of mV. Up to this voltage no current can flow through the quantum dot.

   Above the threshold electrons can tunnel onto the quantum dot and off again, allowing a current to flow.

5. How can the density of excitons be related to a metal-insulator transition?

   Excitons are bound electron-hole pairs. They extend over a certain region in space, thus above a certain density they overlap. Then it does not make sense to assign an electron to a particular hole and the system behaves like a gas of free charge carriers (both electrons and holes) and therefore like a metal.

2. Metal-Insulator Transitions

1. Explain how a structural phase transition can cause a metal-insulator transition.
2. Explain a Mott transition.
3. Explain a Peierls transition.
4. In some materials the Peierls transition is a second order phase transition. In this case, how would the gap grow as a function of temperature?
5. Would there be a Peierls transition in a one-dimensional semiconductor? Explain your reasoning.
6. What properties would a material need to have to exhibit a Mott transition or a Peierls transition?
7. What experiments would you use to determine the type of phase transition? Describe also the experiments you would have to do to determine if it is a first order transition or a second order transition.

Solution

1. Explain how a structural phase transition can cause a metal-insulator transition.

   During a structural phase transition the band structure of the material changes. Therefore it can happen that the Fermi energy is inside a band in one phase and in a band gap in the other phase, meaning that one phase is a metal and the other one an insulator. An example is $\alpha$- and $\beta$-tin.

   Besides, changes in the spacing of the atoms can lead to a Mott transition (see question 1 c) and in quasi one-dimensional materials a certain structural change (dimerization) can lead to a Peierls transition (see c).

2. Explain a Mott transition.

   We know that in solids that consist of atoms with an odd number of valence electrons the upper band is half filled and forms a metallic state, apparently independent of the interatomic distance. However, as Mott put it [ref]:

   "Now for large values of [the interatomic distance] b this is against common experience and, one might say, common sense."

   The reason why this is in fact not true is, that we neglected electron-electron interactions. They lead to screening, which in turn is responsible for a metal-insulator transition. More details are given in question 1.

3. Explain a Peierls transition.

   Peierls transitions happen in one-dimensional crystals at low temperatures. A 1D crystal with lattice constant $a$ the size of the Brioullin zone is $2\pi/a$ and the dispersion relation looks like in the left figure (a).

   If the lattice is distorted like in the right figure (b) at the top, then the periodicity changes to $2a$ and therefore the size of the Brioullin zone reduces to $\pi/a$. The dispersion must still hit the Brioullin zone boundary at 90° and therefore change in the vicinity of the new Brioullin zone boundary like in the right figure.

   

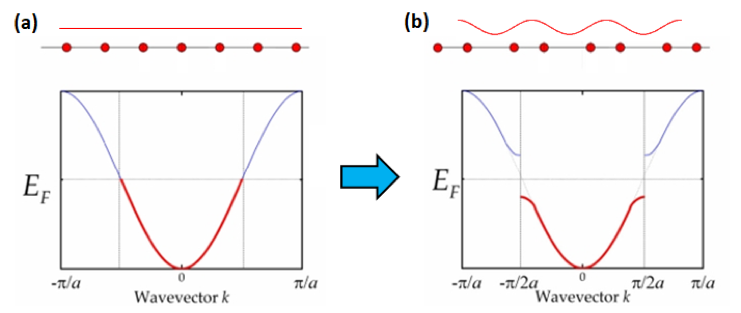   Figure 2: Crystal structure and band structure at a Peierls transition.

   This leads to a band gap and at half filling, as shown in the figure, the Fermi energy is inside the band gap in the distorted lattice. It is evident from the right that the total electronic energy is lower in the distorted case, because the filled states close to the Fermi energy have a lower energy. If this energy gain is high enough to compensate the energy loss from rearranging the ions, then the crystal will spontaneously go through this transition from a metal to an insulator.

   If the crystal is cooled down, the transition happens at a specific temperature, because the effect of the band-splitting is only noticeable when thermal fluctiations can be neglected.

4. In some materials the Peierls transition is a second order phase transition. In this case, how would the gap grow as a function of temperature?

   Since the band gap is zero in the metal phase and non-zero in the insulator phase, it can be used as an order parameter for the phase transition. According to Landau's theory of second order phase transitions the order parameter grows like $\sqrt{T_c-T}$ in the low-temperature phase. Therefore close to the phase transition the band gap should show a $\sqrt{T_c-T}$ dependence.

5. Would there be a Peierls transition in a one-dimensional semiconductor? Explain your reasoning.

   No, because a half filled band is a necessary criterion for a Peierls transition and semiconductors do not have half-filled bands.

6. What properties would a material need to have to exhibit a Mott transition or a Peierls transition?

   For a Mott transition the material must have a rather high electron density, such that the screening effect is strong enough, and there must be a possibility to change the electron density, for example a structural phase transition or doping.

   A Peierls transition can only occur in (quasi-)one-dimensional materials with half-filled bands.

7. What experiments would you use to determine the type of phase transition? Describe also the experiments you would have to do to determine if it is a first order transition or a second order transition.

   A Peierls transition can only occur in quasi one-dimensional materials. For 3D materials this means that they have a strong anisotropy and in particular the conductivity must be much larger in one direction than in the others. This can be checked experimentally and if it is not the case, the observed transition can not be a Peierls transtion.

   Besides, in a Peierls transition the low-temperature phase is insulating and the high temperature phase metallic. For a Mott transition the electron density is relevant and usually the electron density is higher in the low temperature phase. Therefore in a Mott transition we would expect that the low temperature phase is metallic.

   To determine how the structure changed during the phase transition, XRD measurements can be done with both phases.

   The order of the phase transition can be easily determined in a measurement of the order parameter or the specific heat - In a first order phase transition the order parameter is discontinuous and the specific heat diverges, in a second order phase transition the order parameter goes to zero continuously and the specific heat has a jump.

3. One-dimensional potential

Consider electrons moving in a one-dimensional potential. A band of the form $E=-\cos(ka)$ eV is half filled. Here $a$ is the periodicity of the potential.

1. The expression for the current involves the group velocity, the density of states, and a function $f$ that describes the probability that the states are occupied. What is the expression for the current?
2. What are the group velocity and the density of states in this case? How could $f$ be calculated?
3. Under what conditions would this system go through a Peierls transition?
4. Under what conditions would this system go through a Mott transition?

Solution

1. The expression for the current involves the group velocity, the density of states, and a function $\boldsymbol{f}$ that describes the probability that the states are occupied. What is the expression for the current?

   The current is given by the current of a single electron with wave vector $k$ ($-ev_k$) times the number of states at that $k$ times the probability that these states are occupied, integrated over all $k$:

   \begin{equation*} j_{elec}=-e\int v_kD(k)f(k)dk \end{equation*}

2. What are the group velocity and the density of states in this case? How could $\boldsymbol{f}$ be calculated?

   The density of states in $k$-space is constant in one dimension,

   \begin{equation*} D(k)=\frac{2}{\pi} \end{equation*}

   and the group velocity is proportional to the gradient of the dispersion relation,

   \begin{equation*} v_k=\frac{1}{\hbar}\frac{dE}{dk} = \frac{a}{\hbar}\sin(ka) \text{ eV}. \end{equation*}

   The distribution function $f(k)$ can be calculated from the Boltzmann equation, see question 1 in Transport.

3. Under what conditions would this system go through a Peierls transition?

   A Peierls transition is a transition from metallic to insulating state at low temperature which appears in one-dimensional conducting structures (details see question 2).

   

   Figure 3: Dispersion relation for a 1D-material with half filled bands and a periodicity of $a$ (left) and $2a$ (right).

   To perform a Peierls transition the material needs to be quasi one-dimensional and have half-filled bands. It becomes insulating below a certain temperature because a gap appears at the Fermi surface due to the spontaneous pairing of atoms. The period changes from $a$ to $2a$, leading to a change in the size of the unit cell and therefore the Brillouin zone boundary moves.

   Since the present system is one-dimensional and has a half-filled band, it will go through a Peierls transition as soon as the temperature becomes low enough that thermal excitation across the gap becomes negligible.

4. Under what conditions would this system go through a Mott transition?

   Mott transition describes the transition from insulating to metallic state of a material. It appears if the electron density and therefore the electron screening of the coulomb potential changes (details see question 1).

   The important value is the electron density. If it gets high enough and the ground state wave functions of the electrons of neighbouring atoms overlap the material undergoes a Mott transition:

   • small electron density $\rightarrow$ weak screening $\rightarrow$ the electrons are bound and the material is an insulator.
   • large electron density $\rightarrow$ strong screening $\rightarrow$ no bound states and the material is a metal.

   Therefore a material needs to have an electron density which is close enough to the critical density and can be changed to undergo a Mott transition. The electron density may be changed by temperature, pressure, external fields or doping levels in semiconductors.