1. Ferromagnetism

Ferromagnetism can be described by Landau's theory of second order phase transitions.

1. What is the order parameter for ferromagnetism? Sketch the temperature dependence of the order parameter.
2. How could you observe this phase transition in an experiment?
3. How could you calculate the magnetic susceptibility from Landau theory? Sketch the temperature dependence of the magnetic susceptibility.

Solution

1. What is the order parameter for ferromagnetism? Sketch the temperature dependence of the order parameter.

   The order parameter is the magnetization. In a second order phase transition the order parameter always goes to zero like $\sqrt{T_c-T}$ close to the critical temperature (see figure 1).

   

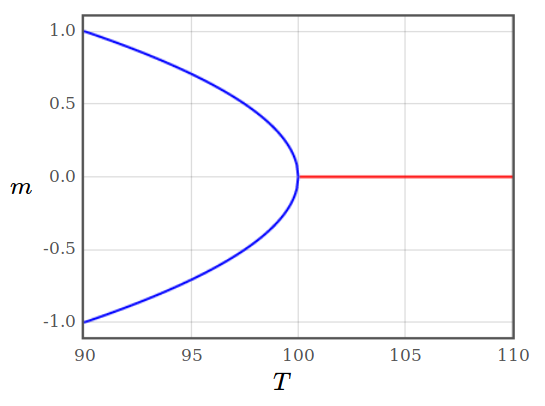   Figure 1: Temperature dependence of the order parameter (magnetization).

2. How could you observe this phase transition in an experiment?

   As the magnetization can be measured (albeit indirectly) by letting the sample vibrate in an induction coil and measuring the induced current, one could continuously measure the magnetization while continuously decreasing the temperature from a point above the critical temperature. When one reaches the critical temperature, one should measure a magnetization, which was not present before.

   Another possibility is to measure the specific heat, because is is straightforward to measure and for a second order phase transition it has a jump at the critical temperature.

3. How could you calculate the magnetic susceptibility from Landau theory? Sketch the temperature dependence of the magnetic susceptibility.

   When using the expansion of $f$ (up to the fourth order, neglecting terms of odd order) to calculate the magnetization $m$ one adds a term $-mB$ for the energy of a magnetic field, resulting in

   \begin{equation*} f\left(T\right) = f_0\left(T\right)+\alpha_0\left(T-T_c\right)m^2+\frac{1}{2}\beta m^4 -mB. \end{equation*}

   For small $m$, one can thus calculate the magnetization (by minimizing the free energy with respect to $m$) as follows:

   \begin{align*} m = \frac{B}{2 \alpha_0 (T-T_{c})}. \end{align*}

   The magnetic susceptibility above the critical temperature can now be calculated as such:

   \begin{align*} \chi = \frac{\partial m}{\partial B} = \frac{1}{2 \alpha_0 (T-T_{c})}. \end{align*}

   Below the critical temperature, there is a finite magnetization and the free energy must be expanded into a Taylor series around this value. This calculation yields

   \begin{equation*} \chi = \frac{1}{4 \alpha_0 (T-T_{c})}. \end{equation*}

   The resulting susceptibility follows the Curie-Weiss-law.

   

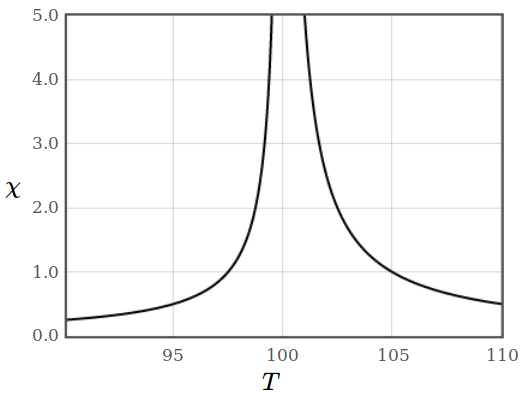   Figure 2: Magnetic susceptibility of a ferromagnet according to Landau's theory of second order phase transitions.