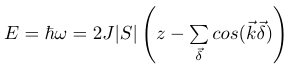
The dispersion relation for magnons in a bcc lattice (exchange energy J, expectation value S for spin) is given by:
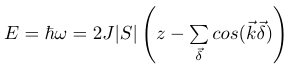
For the next nearest neighbours in bcc with the coordination number z = 8, this yields in:
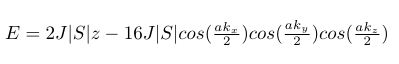
This has the same mathematical form as the dispersion relation for electrons in the tight-binding model:

That means the same data as in the tight-binding calculation can be used, only the scale must be changed by replacing some constants:
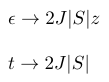
|
The data for the density of states was originally calculated by Thomas Ganner and Klaus Lang here.