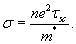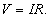
Ohm's law states that the voltage V across a conductor is equal to the current I times the resistance R.
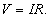
The resistance is related to the resistivity ρ, the width w, the thickness t, and the length L of the sample. The current is assumed to flow along the length of the sample.
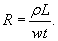
Substituting the expression for the resistance into Ohm's law yields,
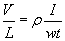
The voltage divided by the length of the sample is the electric field E = V/L and the current divided by the width and the thickness is the current density j = I/(wt). Thus Ohm's law can be written,
E = ρj or j = σE,
where σ is called the conductivity.
The conductivity can be related to the average time between collisions. The force on an electron is,
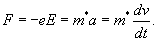
Here F is the force, v is the velocity of the electron and a is the acceleration. If v0 is the velocity just after a collision then the velocity until the next collision will be given by,
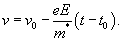
The average velocity is called the drift velocity, vd. If scattering is random, v0 will average to zero. The average value of (t - t0) is called the scattering time, τsc. The drift velocity can then be written as,
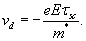
The current density j is related to the average velocity of the electrons, j = -nevd. Using the definition of the drift velocity,
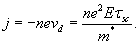
The relationship between the conductivity and the scattering time is therefore,