MAS.020 Introduction to Solid State Physics - 30.01.2026

Problem 1

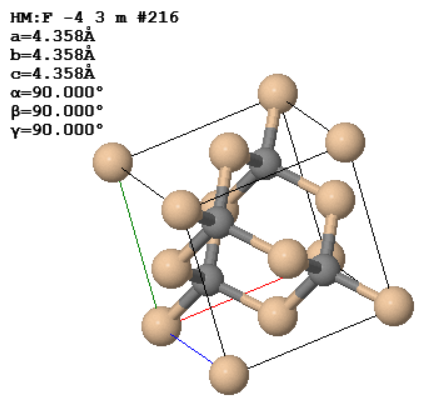
The conventional unit cell of a SiC 3C is shown to the right. The Bravais lattice is fcc.

(a) How many atoms are there in the primitive unit cell?

(b) Draw the atoms in the (110) plane.

(d) How many optical phonon branches does this crystal have?

(e) How could you find the point group symmetries from the information that is given?

Solution

Problem 2

The reciprocal lattice vectors of a crystal can be expressed in terms of the primitive reciprocal lattice vectors,

$$\vec{G}_{hkl} = h\vec{b}_1 + k\vec{b}_2 + l\vec{b}_3,$$

where $h$, $k$, and $l$ are any positive or negative integers. There are an infinite number of reciprocal lattice vectors.

(a) Why are only a finite number of reciprocal lattice vectors measured in an x-ray diffraction experiment?

(b) Why are fewer diffraction peaks measured in a powder diffraction experiment compared to a single crystal diffraction experiment?

(d) For neutron scattering, what determines the $k$-value used in the diffraction condition, $\Delta\vec{k} = \vec{G}$?

(e) Phonons always have a $k$-vector in the first Brillouin zone. If there are $p$ atoms in the primitive unit cell, how many phonon modes share the same $k$-vector?

Solution

Problem 3

(a) What experiments could you perform to determine the band gap of a semiconductor?

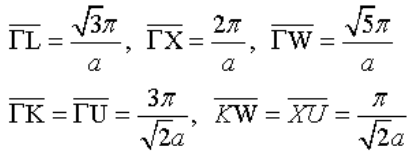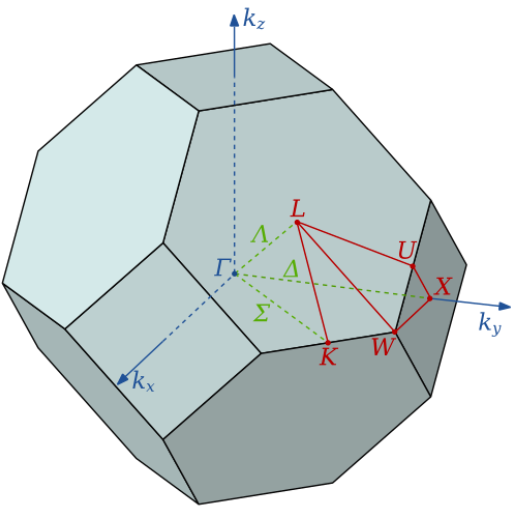
The first Brillouin zone of an fcc metal is shown to the right.

(b) Sketch the lowest electron band, $E$ vs. $k$ dispersion relation, along $X-\Gamma - L - W$. Use the distances given to calculate the energies of the band.

(d) Why are the states close to the Fermi surface most relevant for determining the properties of metals?

(e) What is the formula for the electron contribution to the internal energy density in terms of the density of states?

Solution

(a) Optical absorption, conductivity as a function of temperature. If it is a direct band gap semiconductor, measure the wavelength of light it emits.

(b)
<img src="3b.png" width="400" />

(c) Electron wave functions have the form $\psi = e^{i\vec{k}\cdot\vec{r}}u_{\vec{k}}(\vec{r})$ where $\vec{k}$ is a wavevector in the first Brillouin zone and $u_{\vec{k}}(\vec{r})$ is a periodic function with the periodicity of the primitive unit cell.

(d) All the states with energies a few $k_BT$ below the Fermi energy are always occupied, and all the states with energies a few $k_BT$ above the Fermi energy are always empty. If the occupation does not change as the temperature changes, there will be no contribution to the thermodynamic properties. For every state $\vec{k}$, there is a state $-\vec{k}$ with the same energy. If they are both occupied or both empty, they cancel each other out in any transport phenomena.

(e) The internal energy density is the energy $E$ times the density of states at that energy $D(E)$ times the probability that those states are occupied (the Fermi function $f(E)$), integrated over all energies.

$$u = \int_{-\infty}^{\infty}ED(E)f(E)dE$$

Problem 4

The band structure of Ge is shown below.

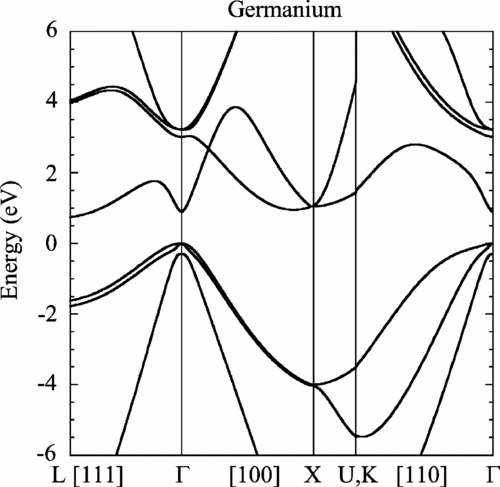
(a) Is germanium a direct band gap or indirect band gap semiconductor?

(b) How large is the band gap in eV?

(d) Sketch the electron density of states for germanium.

(e) Is germanium transparent to visible light? Explain your reasoning.

Solution