Problem 1

Die Gravitationskraft, welche der Mond erfährt, während er um einen Planeten kreist, ist

\( \large \vec{F} =-\frac{Gm_1m_2}{|\vec{r}_2-\vec{r}_1 |^2}\hat{r}_{1\rightarrow 2} \)  [N].

Hier ist $G$ = 6.6726 × 10^-11 N m²/kg² die Gravitationskonstante, $m_1$ =  × 10²⁴ kg ist die Masse des Planeten, $m_2$ =  × 10²¹ kg ist die Masse des Mondes und $\vec{r}_{1\rightarrow 2}$ ist der Einheitsvektor, der vom Planeten zum Mond zeigt.

Die Position des Planeten ist

 [m],

und die Position des Mondes ist

 [m].

Welche Kraft erfährt der Mond?

$|\vec{F}| = $ [N].

Welche Kraft erfährt der Planet?

$|\vec{F}| = $ [N].

Problem 2

Ein Strom der Stärke  A fließt durch eine Solenoidspule in der angegebenen Richtung. Die Spule besitzt 10000 Windungen per Meter. Die Spule ist entlang der $x$-Achse ausgerichtet. Das Zentrum der Spule sei an $y=0$, $z=0$.

Wie groß ist die magnetische Flussdichte innerhalb der Spule?

$|\vec{B}| = $ [T].

Zeichnen Sie einen Pfeil, welcher die Richtung der magnetischen Flußdichte innerhalb der Spule anzeigt.

Ein sich in der $x-y$ Ebene befindendes Elektron (im Bild mit einem gestrichelten Pfeil angedeutet) tritt in die Spule mit einer Geschwindigkeit $\vec{v}= $ $\hat{x}+ $ $\hat{y}+0\,\hat{z}$ [m/s] ein. Wie groß wird die $x$-Komponente der Geschwindigkeit, wenn das Elektron wieder aus der Spule heraustritt?

$v_x = $ [m/s].

Die magnetische Permeabilitätskonstante lautet $\mu_0 = 4 \pi \times 10^{-7}$ Tm/A.

Problem 3

Eine Kugel der Masse $m$ und des Radiuses  cm wird an eine lineare Feder angebracht und oszilliert mit der Bewegung $x(t) = A\sin (\omega t)$. Dabei sei $A$ die Amplitude der Bewegung und $\omega$ die Winkelfrequenz. Die auf die Kugel wirkende Kraft ist $F=-kx$ [N], wobei $k=$ N/m die Federkonstante und $x$ der Abstand von der Gleichgewichtslage ist. Wenn die Kugel sich durch die Gleichgewichtslage an $x=0$ bewegt, dann hat sie die Geschwindigkeit  cm/s. Sobald sich die Kugel jenseits der Gleichgewichtslage befindet, wird sie langsamer und stoppt schließlich, bevor sie ihre Richtung umgekehrt und zur Gleichgewichtslage zurückstrebt. Die Kugel habe bei dem Abstand  cm zur Gleichgewichtslage die Geschwindigkeit Null.

Wie groß ist die Winkelgeschwindigkeit und wie groß ist die Oszillationsfrequenz in Zyklen pro Sekunde? Wie groß ist die Masse der Kugel? Vernachlässigen Sie Reibung.

Problem 4

Schallwellen mit der Wellenzahl $k=$  [1/m] treten durch eine 2 m weiten Öffnung in einer Mauer und werden gebeugt.

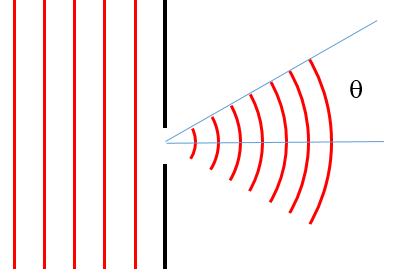
Welche Frequenz kann rechts von der Mauer gehört werden?

$f$ = [Hz].

Unter welchem Winkel wird das erste Minimum im Beugungsmuster im Fernfeld beobachtet?

$\theta$ = [rad]

Die Schallgeschwindigkeit beträgt 340 m/s.

Problem 5

Zwei parallele Metallplatten seien  cm voneinander entfernt. Die linke Platte trägt die Ladung - μC/cm² und die rechte Platte die Ladung  μC/cm². Zwischen den Platten befindet sich Luft.

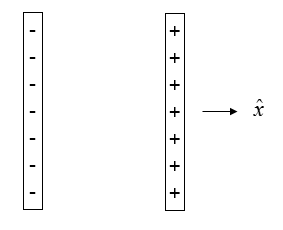
Wie lautet das elektrische Feld zwischen den Platten?

$\vec{E}$ = $\hat{x}$ + $\hat{y}$ + $\hat{z} \; \left[ \text{V/m} \right]$

Die Platten werden auseinanderbewegt, bis ein Endabstand von 20 cm erreicht wird. Wie groß ist die elektrische Spannung zwischen den Platten?

$V$ = [V].

Eine Scheibe aus einem dielektrischen Material wird zwischen die Platten geschoben (welche nachwie vor einen Abstand von 20 cm haben). Die relative dielektrische Konstante lautet $\epsilon_r=3$. Wie groß wird die elektrische Spannung zwischen den Platten?

$V$ = [V].

Die elektrische Feldkonstante $\epsilon_0 = 8.854187817 \times 10^{-12}$ F/m.

Problem 6

Zwei dünne Linsen sind auf einer optischen Achse angeordnet. Die linke Linse hat eine Brennweite von 4 m und die rechte Linse eine Brennweite von 2 m. Die Skizze zeigt die Lage der Brennpunkte der Linsen auf der optischen Achse. Zeichnen Sie den Weg, den einige Lichtstrahlen ausgehend von einem Quellpunkt $o$ nehmen.

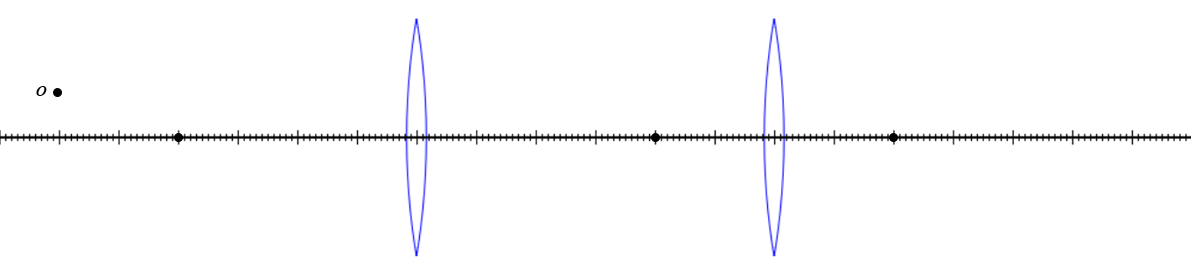
Rechts der rechten Linse entsteht ein Bildpunkt. Ist das Bild reell oder virtuell, aufrecht oder umgekehrt?

Der Abstand der Linsen werde nun vergrößert. Steigt oder verringert sich dabei der Betrag der Vergrößerung?