How the reflections and refractions are calculated

The optical systems page calculates how light rays move through a system of lenses and mirrors. Some details on how the calculations are performed are contained on this page.

Lenses

The lenses used in this simulation have two spherical surfaces and one cylindrical surface. The position of the center of a lens is given by the vector $\vec{r}$ and the orientation of the lens is given by a unit vector $\hat{n}$ that points along the optical axis of the lens. The two spherical surfaces intersect the optical axis at $-d_1\hat{n}$ and $d_2\hat{n}$. The spherical surface that intersects at $-d_1\hat{n}$ has a radius $R_1$ and the center of the sphere lies on the optical axis. $R_1$ is defined to be positive if the center of the sphere is in the positive direction along the optical axis from the intersection point at $-d_1\hat{n}$. The spherical surface that intersects at $d_2\hat{n}$ has a radius $R_2$ and the center of the sphere lies on the optical axis. If the lens is oriented such that $\hat{n}=[1,0,0]$, light rays traveling in the $[1,0,0]$ direction will strike the spherical surface with radius $R_1$ first and then the spherical surface with radius $R_2$. The radius of the cylindrial surface is $R_c$. The index of refraction of the lens is described by a Cauchy model $n=A+B/\lambda^2$. The parameters $A$ and $B$ depend on the material used to make the lens.

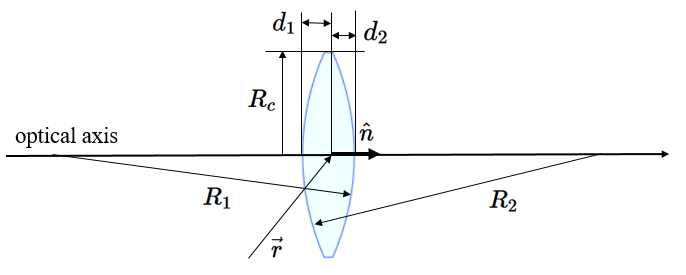
A list of the lenses is kept in an array called lenses. In the code, the $R_1$ value of lens 2 would be lenses[2].R1. To add a lens to this list, press the button for lenses. This executes the command add_lens(r,n,R1,R2,d1,d2,Rc,A,B). For a lens centered at $x = 5,\, y=0\,z =0$ with the optical axis pointing along the positive $x$-direction, with $R_1 = 5$, $R_2 = -5$, $d_1=0.25$, $d_2=0.25$, $R_c=2$, made of fused silica $A = 1.458$, $B=3540$, the command is,

add_lens([5,0,0],[1,0,0],5,-5,0.25,0.25,2,1.458,3540);

Notice that the components of the vectors $\vec{r}$ and $\hat{n}$ are given in square brackets []. The removes the last lens from the list of lenses by executing the command remove_lens().

Spherical mirrors

The spherical mirrors have a radius $R$ and extend a distance $R_c$ from the optical axis. The position $\vec{r}$ of a mirror is where it cuts the optical axis. The orientation of the optical axis is given by a unit vector $\hat{n}$.

A list of the mirrors is kept in an array called mirrors. To add a mirror to this list, press the button for mirrors. This executes the command add_mirror(r,n,R,Rc). The removes the last mirror from the list by executing the command remove_mirror().

Apertures

Because of spherical aberration, it is often necessary to block light that would strike a lens at a large angle from the optical axis. The apertures in this simulation are round plates with a round hole in them. The inner diameter is $R_{in}$ and the outer diameter is $R_{out}$. The position $\vec{r}$ of a aperture is the center of the inner hole. The optical axis is given by a unit vector $\hat{n}$ that is perpendicular to the plane of the aperture. It is assumed that the apertures are made out of an absorbing material so that light does not reflect from them.

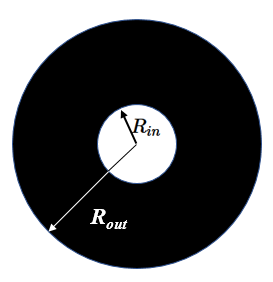
A list of the apertures is kept in an array called apertures. To add an aperture to this list, press the button for apertures. This executes the command add_aperture(r,n,Rin,Rout). The removes the last aperture from the list by executing the command remove_aperture().

Eyes

An eye contains an adaptive lens that can focus nearly parallel light rays on the retina. A typical eye can focus on distant objects and objects that are brought no closer than the near point at 25 cm from the eye. The position of the image in the eye changes only about 1 mm as an object is moved from the near point to far away. Because of this it is hard to understand when a microscope or telescope is in focus if the eye is not included in the simulation.

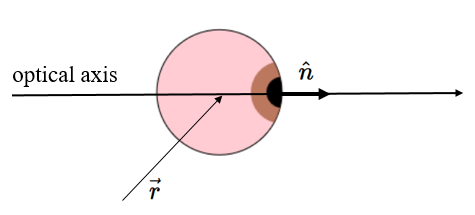
An eye is a complicated construction and only a simple model for it is used here. An eye is defined as a sphere with a radius of 2.4 cm. The center of the sphere is at position $\vec{r}$ and the direction that the eye is looking in given by a unit vector $\hat{n}$. Since the eye is an adaptive lens, we define a parameter $f$ to specify how the eye is focused. $f$ is the distance from the front of the lens of the eye to the point where parallel rays are focused when the eye is in air. When $f = 2.4$ cm, they eye will focus rays from a distant object on the retina. If an object is brought to the near point at 25 cm, $f$ must be adjusted to 2.295 to bring the object in focus.

A list of the eyes is kept in an array called eyes. To add an eye to this list, press the button for eyes. This executes the command add_eye(r,n,f). The removes the last eye from the list by executing the command remove_eye().

Walls

It is possible to introduce light absorbing walls that define the extent of the laboratory. A wall is defined by a point on the wall $\vec{r}$ and a normal vector to the wall $\hat{n}$. Such a wall is an infinite plane so more walls are needed to define a finite volume for the laboratory.

A list of the wall is kept in an array called walls. To add a wall to this list, use the command add_wall(r,n). To remove the last wall from the list use the command remove_wall().

Ray segments

The light rays travel in straight lines until they reflect or refract. Each of the straight sections is a ray segment. A ray segment is defined by a starting point $\vec{r}_0$, a unit vector pointing in the direction that the light propagates $\hat{n}$, an intensity, $I$, and a wavelength in nanometers. The ray segments are put into a list called rays.

There are some functions to add ray segments. The command add_single_ray(r,n,wavelengths) adds ray segments that start at $\vec{r}$ and travel in a direction $\hat{n}$. The variable wavelengths is a list of wavelengths in nanometers for example, [450,510,650]. The square brackets are necessary even if there is only one wavelength in the list. A ray segement will be generated for every wavelength in the list.

There is a function add_point_source(r,n,wavelengths,theta) that adds 48 rays all starting at $\vec{r}$ at angles equally distributed from -theta to theta around the direction given by $\hat{n}$.

There is a function add_beam(r,n,wavelengths) that adds a beam 1 cm wide of parallel rays that start at $\vec{r}$ and point in the direction $\hat{n}$.

To calculate the endpoint of a ray segment it necessary to determine which surface it strikes. We define a minimum distance and initially set it to a large value like dmin = 10000 and then go through the lists of lenses, mirrors, apertures, eyes, and walls to see if the ray strikes any of them at a shorter distance. If the ray segment strikes one of these objects at a distance $d < d_{min}$, then minimum distance is set to this value and we continue through the lists looking of the shortest distance.

The lenses have two spherical surfaces and one cylindrial surface. The spherical mirrors have one spherical surface. The condition that a line, $\vec{r}_0 + d\hat{n}$, intersects a sphere centered at $\vec{r}$ with a radius $R$ is,

Calculating the inner product we have,

This can be solved for $d$ using the quadratic equation,

The function that performs this calculation is,

function intersect_line_sphere(r0,n,R,C) { //find the intersection of a line and a sphere
  // r0 is the intitial point on the line, n is the unit vector in the direction of the line
  // R is the radius of the sphere, C is the center point of the sphere
  let b = dot(n,vsub(r0,C));
  let q  = dot(vsub(r0,C),vsub(r0,C)) - R*R;
  let Delta = b*b - q;
  if (Delta > 0) {
    let d1 = -b + Math.sqrt(Delta);
    let d2 = -b - Math.sqrt(Delta); 
    return [d1,d2];
  }
  else {
    return null;
  }
}

The calculation makes use of some vector functions.

function dot(A,B) {  //calculate the dot product of vectors and scalars
  let c= [];
  let x;
  if ((Array.isArray(A))&(Array.isArray(B))) { \\dot product of two vectors, the result is a scalar
    x = A[0]*B[0] + A[1]*B[1] + A[2]*B[2];
   return x;
  }
  if ((Number.isFinite(A))&(Array.isArray(B))) { \\ A is a scalar, B is a vector, the result is a vector
    c[0] = A*B[0];
    c[1] = A*B[1];
    c[2] = A*B[2];
    return c;
  }
  if ((Number.isFinite(B))&(Array.isArray(A))) { \\ B is a scalar, A is a vector, the result is a vector
    c[0] = B*A[0];
    c[1] = B*A[1];
    c[2] = B*A[2];
    return c;
  }
  if ((Number.isFinite(A))&(Number.isFinite(B))) { \\ A is a scalar, B is a scalar, the result is a scalar
    x = A*B;
    return x;
  }
}

function length(A) {  // determine the length of vector A
  let L = Math.sqrt(A[0]*A[0] + A[1]*A[1] + A[2]*A[2]);
  return L;
}

function unit(A) { // determine the unit vector pointing in the direction of vector A
  let u = [];
  let L = Math.sqrt(A[0]*A[0] + A[1]*A[1] + A[2]*A[2]);
  u[0] = A[0]/L;
  u[1] = A[1]/L;
  u[2] = A[2]/L;
  return u;
}

function vadd(A,B) { // add vectors A and B, A+B
  let c = [];
  c[0] = A[0]+B[0];
  c[1] = A[1]+B[1];
  c[2] = A[2]+B[2];
  return c;
}

function vsub(A,B) { // subtract vector B from A, A-B
  let c = [];
  c[0] = A[0]-B[0];
  c[1] = A[1]-B[1];
  c[2] = A[2]-B[2];
   return c;
}

After the intersections of the line and the sphere have been determined, it is necessary to use some if statements to determine if the intersection is on the part of the sphere that forms the lens. A similar calculation is perfomed for the cylindrical surfaces. The condition that a line, $\vec{r}_0 + d\hat{n}$, intersects a cylinder with an axis $\hat{n}_c$, a radius $R_c$, with a point on the axis $\vec{r}$ is,

This can be solved for $d$. The function that performs this calculation is,

function intersect_line_cylinder(r0,n,R,C,nc) { //find the intersection of a line and a cylinder
  // r0 is the intitial point on the line, n is the unit vector in the direction of the line
  // R is the radius of the cylinder, n is the unit vector along the central axis, C is a point on the central axis
  let r1 = vsub(r0,C); 
  let r1dotnc = dot(r1,nc);
  let rpara = dot(r1dotnc,nc);
  let rperp = vsub(r1,rpara);
  let ndotnc = dot(n,nc);
  let npara = dot(ndotnc,nc);
  let nperp = vsub(n,npara);
  let a = dot(nperp,nperp); 
  let b = 2*dot(nperp,rperp);
  let c = dot(rperp,rperp) - R*R;
  if ((b*b - 4*a*c) > 0) {
    return [(-b + Math.sqrt(b*b - 4*a*c))/(2*a), (-b - Math.sqrt(b*b - 4*a*c))/(2*a)];
  }
  else {
    return null;
  }
}

Again it is necessary to use some if statements to determine if the intersection is on the part of the cylinder that forms the lens. For the apertures and walls it is necessary to calculate the intersection of a line and a plane. The condition that a line, $\vec{r}_0 + d\hat{n}$, intersects a plane with normal $\hat{n}_p$, with a point on the plane $\vec{r}$ is,

This can be solved for $d$. The function that performs this calculation is,

function intersect_line_plane(r0,n,p0,np) { //find the intersection of a line and a plane
  // r0 is the intitial point on the line, n is the unit vector in the direction of the line
  // p0 is a point on the plane and np is the unit normal to the plane
  let ndotnp = dot(n,np);
  if (ndotnp == 0) {
    return null;  // the line and plane are parallel
  }
  else { 
    let d = dot(np,vsub(p0,r0))/ndotnp;
    return d;
  }
}

Once we have gone through the whole list of objects that a ray segment can strike and have determined which is the closest, the endpoint is,

Reflection and refraction

If the endpoint of a ray segment is on a aperture or a wall, we do nothing and go on to calculate the endpoint of the next ray segment in the list. However, if the enpoint is on a lens or a mirror or on the pupil of an eye, we need to calculate the reflected and refracted ray segments. The reflected ray and refracted rays lie in the plane defined by the ray segment that strikes the surface and the normal to the surface $\hat{n}_s$. The normal of the ray segment can be decomposed into a component parallel to the surface normal $\hat{n}_{\parallel}$ and perpendicular to the normal $\hat{n}_{\perp}$.

The normal vector of the reflected ray is generated by inverting the parallel component,

The reflected ray is added to the list of ray segements. The wavelength of the reflected ray is the same as the incoming ray. If the reflection is from a mirror or due to total internal reflection, the intensity of the reflected ray is the same as the incoming ray. However, if the incoming ray refracts at the surface of a lens, the intensity of the reflected ray only has a small fraction of the intensity of the incoming ray. The default intensity for a reflected ray in this case is 0.1 times the intensity of the incoming ray.

The refracted ray can be calculated using Snell's law, $n_1\sin\theta_1 = n_2\sin\theta_2$.

The unit vector in the direction of the refracted ray is,

The refracted ray is added to the end of the list of ray segements with the same wavelength as the incoming ray and 0.9 times the intensity of the incoming ray.

If these reflected and refracted rays strike a mirror or a lens, more ray segments will be generated and put a the end of the list. This way multiple reflections are included in the calculation.

Commands to include optical components and initial rays to the system can be typed into the textarea with the blue border below. The command calculate_rays() calculates the reflections and refractions. The command list_rays() outputs a list of the ray segments that have been calculated. Use the buttons to load some examples.