Einfachspaltexperiment
|
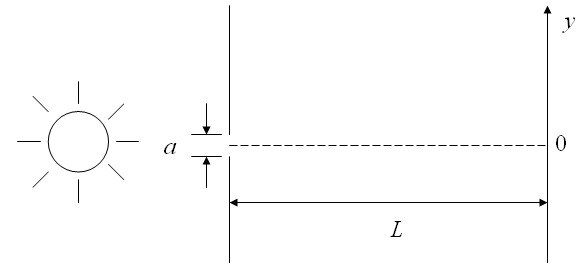
In a single slit experiment, waves pass through a narrow slit of width $a$. The interference pattern is observed on a screen that is a distance $L$ from the slit.
| |
|
Die kleine Teilung des rechten Maßstabes ist in mm.
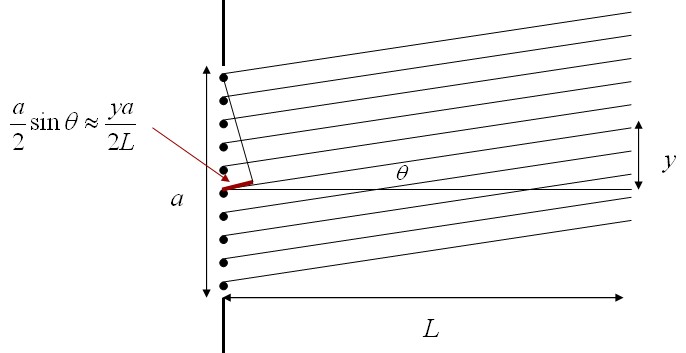
Einen Einfachspalt kann man als sich aus vielen kleinen Quellen aufgebaut denken. Diese Quellen sind im Diagramm als Punkte dargestellt. Die Amplituden der Wellen aus jeder dieser Quellen ist (E0/a)dy. Die Wellen von jeder dieser Quellen werden abhängig vom Winkel θ eine verschiedene Phase besitzen, wenn sie am Schirm auftreffen. Diese Phase ist -2πysin(θ)/λ = -βy/a, wobei β eine Konstante ist: β = 2πasin(θ)/λ. Die Beiträge aller Quellen zur Gesamtamplitude ist durch das folgende Integral gegeben:
Das Ausführen der Integration ergibt:
| E = |
|
eiωt(eiβ/2 - e-iβ/2) = |
|
eiωtsin(β/2) |
Das Quadrat der Amplitude ist
Da die Intensität proportional zur Quadrat der Amplitude ist:
Fernfeld
Im Fernfeld, d.h. wenn $L > > \lambda$ und $L > > y$, entsteht destruktive Interferenz für $n\lambda=\frac{ay}{L}$ mit ganzzahligem $n \ne 0$.
| 
