A block slides down an inclined plane

A block of mass $m$ is put on an inclined plane that makes an angle of $\theta$ degrees from horizontal.

The gravitational force, $-mg\hat{y}$ can be decomposed into a force normal to the inclined plane and a force parallel to the inclined plane.

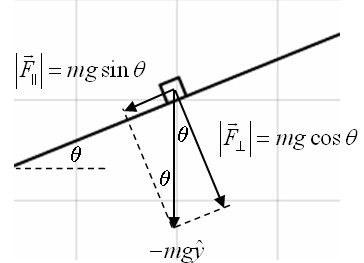
The force parallel to the plane, $|F_{\parallel}|=mg\sin\theta$, causes the block to slide along the plane. In terms of its $x$- and $y$-components, the force along the plane is,

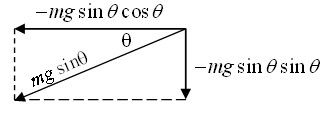
$\vec{F}_{\parallel} = -mg\sin\theta\cos\theta \hat{x} - mg\sin\theta\sin\theta \hat{y}.$

This is a constant force; it is independent of the position, the velocity, and the time. We expect the mass to exhibit parabolic motion and formulas for the position vector and the velocity vector can be found on the page Constant Force = Parabolic Motion. It is of course also possible to put this force and the initial conditions in a numerical differential equation solver. The force and the mass is loaded into the differential solver below every time the sliders are adjusted. A drag force can be added to the differential equation solver by adding a term to the force that is in the opposite direction of the velocity. If this drag force is linear $\vec{F}_{drag} = -a\vec{v}$, then it is possible to find formulas to describe the resulting motion. However, if the drag force is nonlinear such as, $\vec{F}_{drag} = -a|\vec{v}|\vec{v}$, no simple formulas can be found and a numerical differential equation solver is the best option.

No drag force: $\vec{F} = -mg\sin\theta\cos\theta \,\hat{x} - mg\sin\theta\sin\theta \,\hat{y}$
Linear drag force: $\vec{F} = -mg\sin\theta\cos\theta\, \hat{x} - mg\sin\theta\sin\theta \,\hat{y}-a\vec{v}$
Nonlinear drag force: $\vec{F} = -mg\sin\theta\cos\theta \,\hat{x} - mg\sin\theta\sin\theta \,\hat{y}-a|\vec{v}|\vec{v}$