Optics

Optics is the study of light waves and these waves interfere and diffract as was described in the waves section. Recall from the discussion of a single slit of width $a$ that the central maximum diverges with an angle $\theta \approx \frac{\lambda}{a}$.

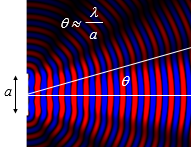
For most lens systems the apertures are on the order of millimeters while the wavelength is on the order of hundreds of nanometers. This means that the divergence angle will typically be small, $\theta \approx 10^{-4}$ rad. Because the divergence of the light beam is so small, we can consider that light travels in straight light beams (or light rays). The limit where all of the optical components (lenses, apertures) are much larger than the wavelength is called geometric optics and we will restrict ourselves to this limit in this chapter. There are only two fundamental principles in geometric optics, reflection and refraction. When a light ray reflects off a surface, the incoming angle $\theta_1$ is equal to the outgoing angle $\theta_2$.

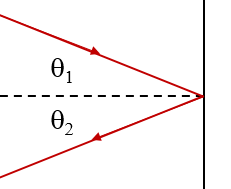
Here both angles are measured with respect to the normal to the surface that the light ray reflects off.

The other fundamental principle of geometric optics is Snell's law of refraction. When a light ray passes from a medium with an index of refraction $n_1$ to a medium with index of refraction $n_2$, the light ray is bent according to,

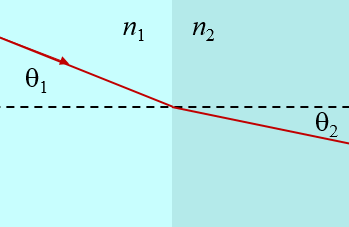
Here the angles are measured with respect to the normal to the interface and are measured in radians.

All of geometric optics can be derived from these two principles.