Oscillations

Oscillations are typically described using differential equations. In the section on motion, we solved the differential equations using a numerical solver. Given the intitial conditions, the solver found the solutions by making small time steps forward. We will continue to use numerical solvers in this section but sometimes it is possible to find analytic solutions to a differential equation. In those cases you can write down a formula for the position and the velocity of a particle executing an oscillation. We will also examine forced oscillators and describe the mathematical details of a resonance.

Simple harmonic motion was already discussed in the section on motion. The differential equation that describes simple harmonic motion is,

Here $m$ [kg] is the mass and $k$ [N/m] is the spring constant.This is a statement of Newton's law; mass times acceleration equals the spring force. If a damping force is added, the differential equation becomes,

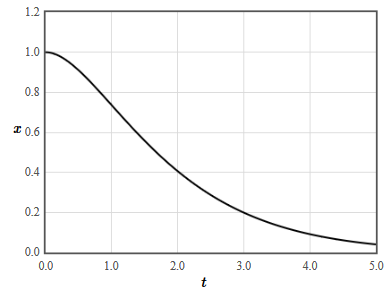
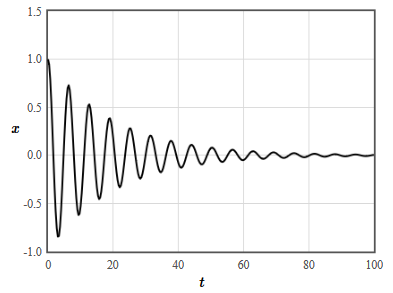
Here $b$ [N s/m] is the damping constant and the damping force is proportional to the velocity. The form of the solutions depends how how large the damping constant $b$ is. The damping decreases the frequency of the oscillations until a critical damping where no more oscillations occur and there is only exponential damping. There are four cases.

• $b = 0$: undamped oscillations, $\omega = \sqrt{\frac{k}{m}}$ rad/s. $$x(t) = x_0\cos (\omega t) +\frac{v_{x0}}{\omega}\sin (\omega t).$$

• $4mk - b^2 > 0$: underdamped oscillations, $\omega=\frac{\sqrt{4mk-b^2}}{2m}$ rad/s, $\tau=\frac{2m}{b}$ s. $$x(t) = \exp \left(-t/\tau\right)\left(x_0\cos (\omega t) + \left(\frac{v_{x0}}{\omega}+\frac{x_0}{\omega\tau}\right)\sin(\omega t)\right).$$

• $4mk - b^2 = 0$: critical damping, $\tau=\frac{2m}{b}$ s. $$x(t) = x_0 \exp \left(-t/\tau\right)+\left(v_{x0} + \frac{x_0}{\tau}\right)t \exp \left(-t/\tau\right).$$

• $4mk - b^2 < 0$: overdamped , $\tau_1=\frac{2m}{b-\sqrt{b^2-4km}}$ s, $\tau_2=\frac{2m}{b+\sqrt{b^2-4km}}$ s. $$x(t) = \frac{v_{x0}\tau_1\tau_2 + x_0\tau_1}{\tau_1-\tau_2} \exp \left(-t/\tau_1\right)- \frac{v_{x0}\tau_1\tau_2 + x_0\tau_2}{\tau_1-\tau_2}\exp \left(-t/\tau_2\right).$$


Here $x_0$ is the position at $t=0$ and $v_{x0}$ is the velocity at $t=0$.