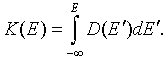
The electron density n is the integral of the density of states D(E) times the probability that those states are occupied. The occupation probablility is given by the Fermi function f(E).
This relation implicitly defines the chemical potential μ. If the electron density and the density of states are known, the chemical potential can be determined by guessing a chemical potential, evaluating the integral numerically and comparing the result with the known electron density. If the calculated electron density is too low, a larger chemical potential must be guessed. If the calculated electron density is too large, a smaller chemical potential must be guessed. This process is continued until the chemical potential is determined to the desired accuracy.
The chemical potential at zero temperature is called the Fermi energy Ef. See: Calculating the Fermi energy of a metal from the density of states.
The numerical calculation goes faster if we first integrate by parts.
\[ \begin{equation} n=\int\limits_{-\infty}^{\infty} D(E)f(E)dE = K(\infty)f(\infty)-K(-\infty)f(-\infty)-\int\limits_{-\infty}^{\infty} K(E)\frac{f(E)}{dE}dE. \end{equation} \]Here the function K(E) is,
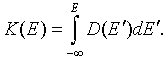
The boundary terms vanish because K(-∞) = 0 and f(∞) = 0. The electron density can then be written as,
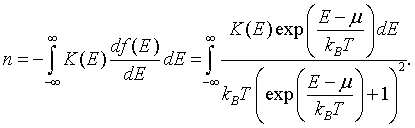
This is a convenient form since the derivative of the Fermi function df/dE is only significantly different from zero in the range from μ - 7kBT to μ + 7kBT.
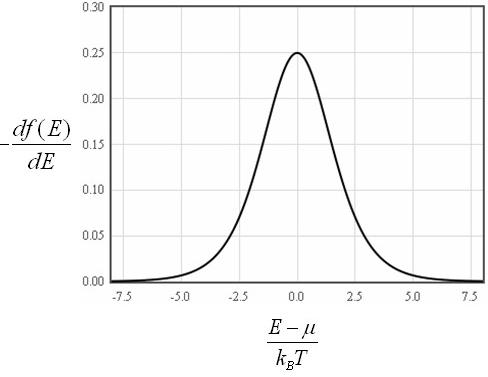
This means that the electron density can be approximated as,
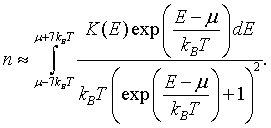
For metals, the integral of the density of states K(E) is a monotonically increasing function of energy. See: Calculating the integral of the density of states to make plots of K(E). If K(E) is known at a set of discrete points, K(E1), K(E2),...K(EN), then the electron density can be approximated as,
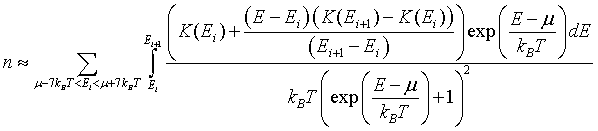
The integral can be performed to yield,
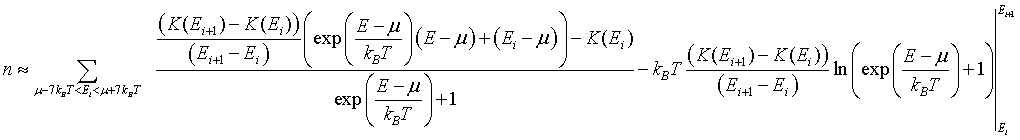
The form below can be used to calculate the chemical potential from the density of states. The density of states is input as two columns of text in the lower left textbox. The first column is the energy in eV. The second column is the density of states. The units of the density of states depend on the dimensionality. In one dimension the units are eV-1 m-1, in two dimensions the units are eV-1 m-2, and in three dimensions the units are eV-1 m-3. After the 'DoS → μ' button is pressed, the density of states is plotted on the left and the chemical potential is plotted on the right. The data for the chemical potential plot also appears in the lower right textbox. The first column is the temperature in Kelvin. The second column is the chemical potential in units of eV.
| D(E) [eV-1 m-3] | μ [eV] | Steps in the plot of μ vs. T are an artifact of the calculation that occurs when the chemical potential is nearly constant.
| |||
E [eV] | T [K] |
