Phonon density of states for a 1-d linear chain with two masses

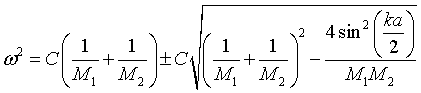
The phonon density of states can be calculated numerically from the dispersion relation,

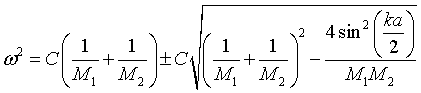
For this calculation, the frequency range from ω = 0 to the maximum frequency ω_max = √2C(1/M1 + 1/M2) is divided into 300 intervals. The frequencies are calculated for 10000 equally spaced values of k bewteen k = 0 and k = π/a. For each value of k there are two frequencies, one on the acoustic branch and one on the optical branch. The program counts how many times the frequency falls in each of the 300 frequency intervals to calculate the density of states.