4.2 Madelung constant of a two-dimensional crystal
4.5 Madelung constant in one dimension
4.1 Coulomb interaction
The molecule HF (hydrofluoric acid) has a bond length of 0.092 nm. The molecule is characterized by a very strong partial charge transfer of an electron from hydrogen to fluorine of 0.41 $e$. A sodium ion (Na+) is 0.2 nm away from the HF molecule. Calculate how much energy it would take to move the Na+ far to the right of the molecule. Assume that the atoms remain in a line.
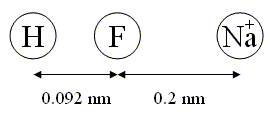
0.9301 eV.
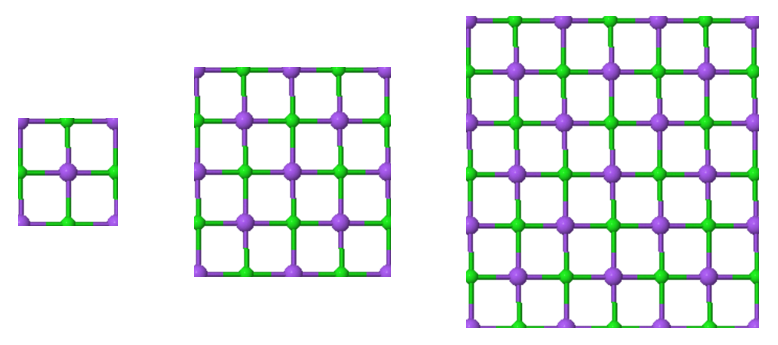
4.2 Madelung constant of a two-dimensional crystal
Determine the Madelung constants of the different sections of the two-dimensional ionic crystal in the figure below. Compare the results with the Madelung constants of the infinite crystal $(\alpha = 1.6155)$. Why are the sections selected with the atoms at the border of the sections truncated?
4.3 Cohesive energy
The cohesive energy of a crystal is the energy needed to separate all of the atoms. The cohesive energy of NaCl can be described by the function,
\begin{equation} U_{tot}= N\left(z\lambda e^{-R/\rho}-\frac{\alpha e^2}{4\pi\epsilon_0 R}\right). \end{equation}Here $N$ is the number of primitive unit cells in the crystal, $R$ is the interatomic spacing, $z$ is the number of nearest neighbors, $\lambda,\rho$, and $\alpha$ are constants. For NaCl, $\rho = 0.321$ Å, $z\lambda = 1.05\times 10^{-15}$ J, and $\alpha = 1.747$.
(a) Determine the lattice constant of the conventional unit cell from this expression.
(b) Calculate the effective spring constant of a single bond.
(c) Calculate the bulk modulus $B = -V(dp/dV)$ and the compressibility $\kappa = 1/B$ of an ideal sodium chloride crystal at $T = 0$ K. Here $V$ is the volume and $p$ is the pressure. At $T = 0$ K, the entropy is zero so the total cohesive energy is $dU_{tot} = -p dV$. This means that the bulk modulus at low temperature is,
\begin{equation} B= V\frac{d^2U_{tot}}{dV^2}. \end{equation}$B= 2.418\times 10^{10}$ N/m². The compressibility is $\kappa = \frac{1}{B} = 4.136 \times 10^{-11}$ m²/N.
4.4 Madelung constant
The CsCl structure has the largest Madelung constant and therefore ionic crystals forming this structure have the lowest energy. Explain why some ionic crystals form the NaCl or Zincblend crystal structures instead of the low energy CsCl structure.
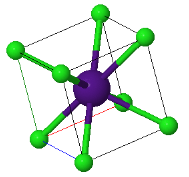 | 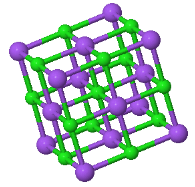 | 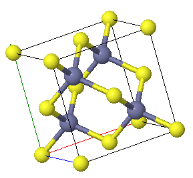 |
CsCl | NaCl | Zincblend |
What is the critical ratio of the ionic radii where zincblende becomes unstable?
4.5 Madelung constant in one dimension
Calculate the Madelung constant $\alpha$ of a linear chain of ions with alternating positive and negative charges $q$. The ion separation is 1 Å.
4.6 Madelung constant of a 2d hexagonal lattice
Determine the Madelung constants of the two sections of a two dimensional ionic crystal in the figure below. Compare the results with the Madelung constants of the infinite crystal $(\alpha= 1.542)$. Why are the sections selected with the atoms at the border of the sections truncated?
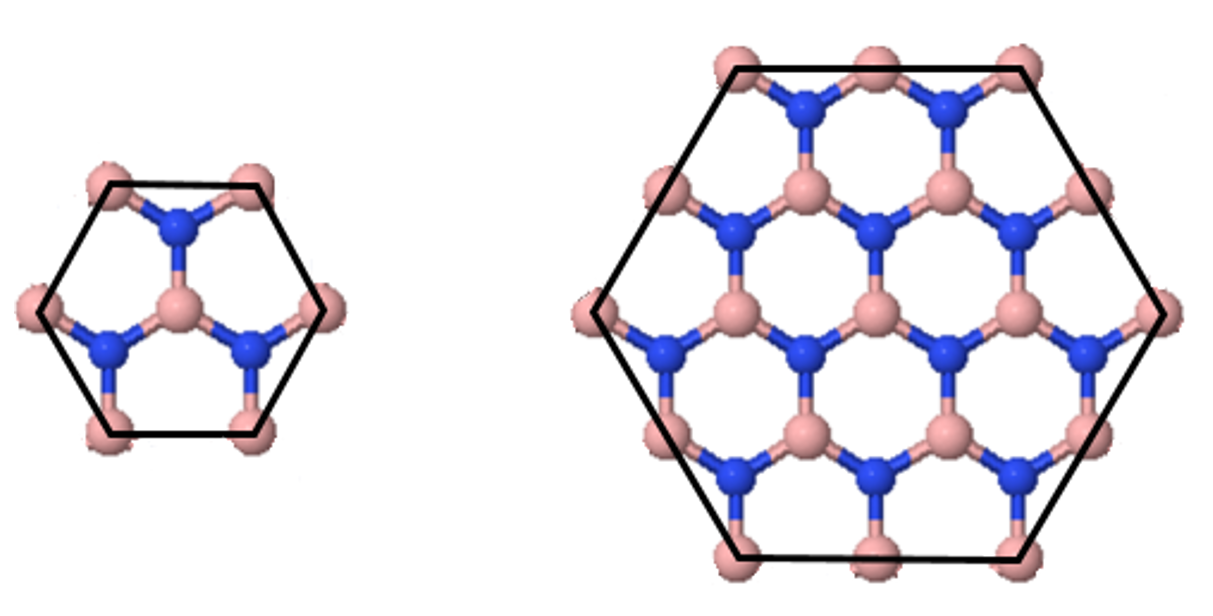
What is the critical ratio of the ionic radii where a 2d hexagonal lattice becomes unstable?