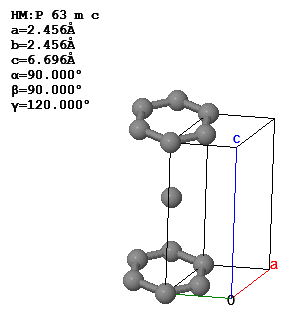
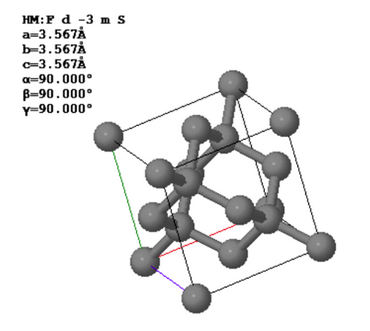
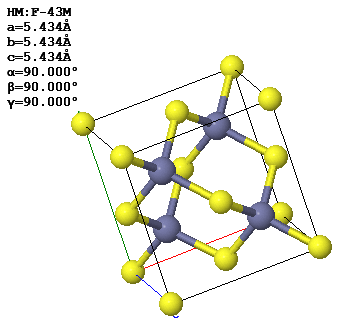
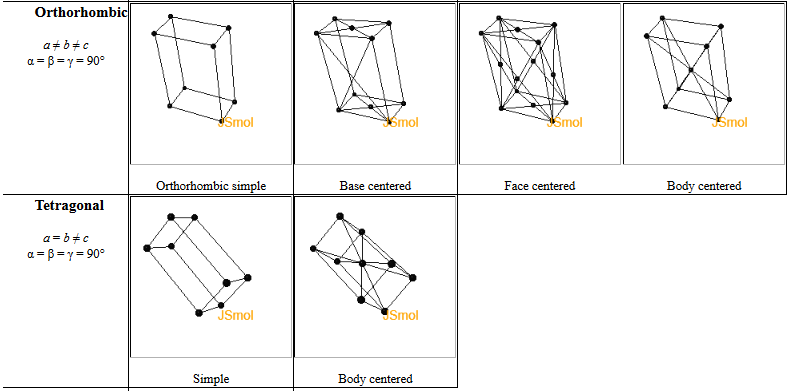
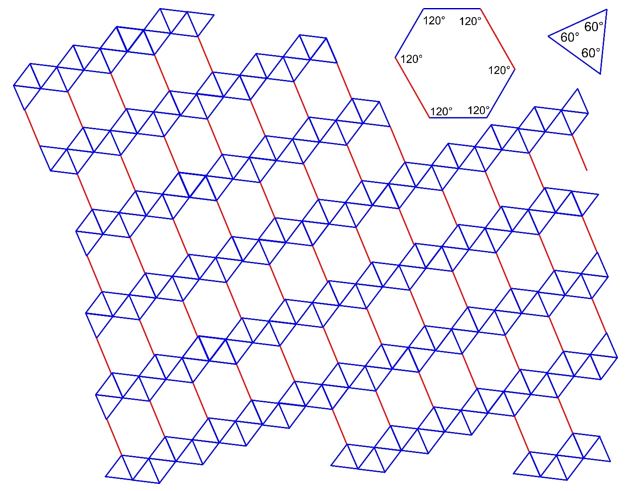
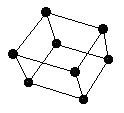
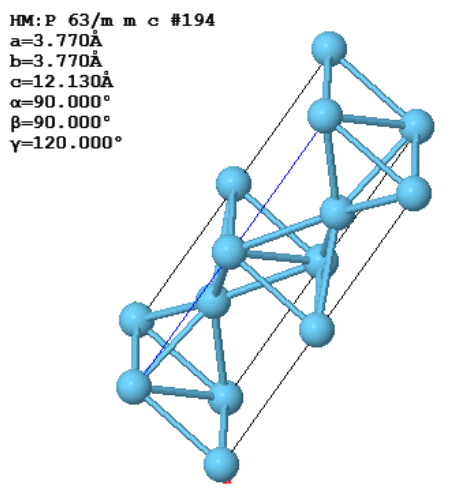
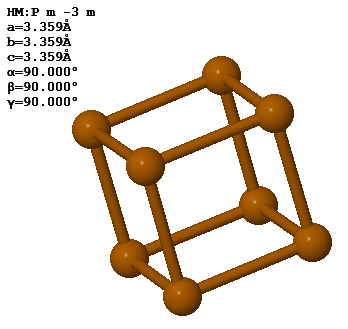In a crystal, atoms are arranged in straight rows in a three-dimensional periodic pattern.
A small part of the crystal that can be repeated to form the entire crystal is called a unit cell.
Asymmetric unit
| 
Primitive unit cell
| 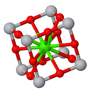
Conventional unit cell
| 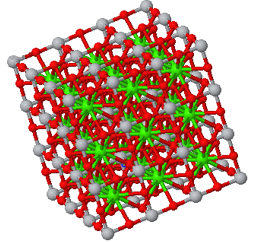
Crystal
|
A crystal can be specified in several ways. One way is to repeat the primitive unit cell at each translation vector,
$$\vec{T} = h\vec{a}_1 + k\vec{a}_2 + l\vec{a}_3$$
Here $\vec{a}_1$, $\vec{a}_2$, $\vec{a}_3$ are the primitive lattice vectors and $h$, $k$, and $l$ are integers. The primitive lattice vectors are not unique; different choices for the primitive lattice vectors are possible.
Another common way to specify crystal is to give the lattice parameters $(a,b,c,\alpha,\beta,\gamma )$, the space group, and the asymmetric unit. The lattice parameters $a$, $b$, and $c$ are the lengths of the sides of a parallelepiped; $\alpha$ is the angle between $b$ and $c$; $\beta$ is the angle between $a$ and $c$; and $\gamma$ is the angle between $a$ and $b$. This parallelepiped can have a larger volume than the primitive unit cell. If it is possible to use a cubic unit cell, crystalographers use the smallest possible cube as the conventional unit cell. For simple cubic, the conventional unit cell is the primitive unit cell but for bcc, the conventional unit cell is twice the volume of the primitive unit cell and for fcc, the conventional unit cell has four times the volume of the primitive unit cell. The asymmetric unit is the minimum number of atoms you need to specify to create the basis by applying the symmetries of the space group to the asymmetric unit.
Miller indices
Every point of a Bravais lattice can be reached from the origin by a translation vector of the form,
\[ \begin{equation}
\vec{T}_{hkl} = h\vec{a}_1 + k\vec{a}_2 + l\vec{a}_3,
\end{equation} \]
where $\vec{a}_1$, $\vec{a}_2$, $\vec{a}_3$ are the primitive lattice vectors and $h$, $k$, and $l$ are integers called the Miller indices. The direction that the vector $\vec{T}_{hkl}$ points is denoted with square brackets, $[hkl]$. If there are directions that are equivalent due to symmetry any of the equivalent directions are specified by angular brackets <$hkl$>.
For example, in a cubic system:
<100> = [100], [010], [001], [-100], [0-10], [00-1]
<110> = [110], [-1-10], [1-10], [-110], [101], [-10-1], [-101], [10-1], [011], [0-1-1], [0-11], [01-1].
Often the minus signs are drawn as overlines [-10-1] = $\left[\overline{1}0\overline{1}\right]$. This is pronounced one-bar zero one-bar.
Planes
Using Miller indices, planes are denoted with curved brackets $(hkl)$. The $(hkl)$ plane intercepts the axis in the direction of $\vec{a}_1$ at $\frac{|\vec{a}_1|}{h}$, the axis in the direction of $\vec{a}_2$ at $\frac{|\vec{a}_2|}{k}$, and the axis in the direction of $\vec{a}_3$ at $\frac{|\vec{a}_3|}{l}$.
Equivalent planes are denoted with curly brackets $\{hkl\}$. Three points that can be used to define the $(hkl)$ plane are $\left( \frac{a_{1x}}{h},\frac{a_{1y}}{h},\frac{a_{1z}}{h} \right)$, $\left(\frac{a_{2x}}{k},\frac{a_{2y}}{k},\frac{a_{2z}}{k} \right)$, and $\left(\frac{a_{3x}}{l},\frac{a_{3y}}{l},\frac{a_{3z}}{l}\right)$. The normal vector to this plane can be determined by taking the cross product of two vectors in the plane. If $(h,k,l \ne 0)$, two suitable vectors are $\vec{v}_1=\frac{\vec{a}_1}{h}-\frac{\vec{a}_3}{l}$ and $\vec{v}_2=\frac{\vec{a}_2}{k}-\frac{\vec{a}_3}{l}$. The unit vector normal to the $(hkl)$ plane is,
$$\hat{n}_{hkl}=\frac{\vec{v}_1\times \vec{v}_2}{|\vec{v}_1\times \vec{v}_2|}.$$
For cubic crystals, $\vec{T}_{hkl}$ is normal to $(hkl)$ and parallel to $\hat{n}_{hkl}$ but this is not generally true for crystals with other symmetries.
The normal vector to a plane
The set of planes perpendicular to a vector \(A_x\hat{x}+A_y\hat{y}+A_z\hat{z}\) is,
$$A_xx+A_yy+A_zz = C,$$
where \(C\) is any constant. If a point \( (x_0,y_0,z_0)\) on the plane is known, \(C\) can be calculated,
$$C=A_xx_0+A_yy_0+A_zz_0.$$
The app below will solve 3 linear equations for three unknowns. (It determines the point where three planes intersect.)
In two dimensions, a Bravais lattice has two primitive lattice vectors \(\vec{a}\) and \(\vec{b}\). The lengths of these vectors are the lattice constants \(a\) and \(b\).The angle between the primitive lattice vectors is \(\gamma\). There are five two-dimensional Bravais lattices,
- cubic: \(a = b\), \(\gamma\) = 90°.
- hexagonal: \(a = b\), \(\gamma\) = 120°.
- rectangular: \(a \neq b\), \(\gamma\) = 90°.
- rectangular centered: \(a \neq b\), \(\gamma\) = 90° and two lattice points per unit cell.
- oblique: \(a \neq b\), \(\gamma \neq \) 90°.
If more than one Bravais lattice can be used to describe a periodic structure, there are priority rules to determine the 2D Bravais lattices.
- Use the Bravais lattice with the highest symmetry (cubic > hexagonal > rectangular > oblique).
- Use the Bravais lattice with smallest unit cell area.
- Use the Bravais with the smallest lattice constants a and b.
- Use \(a \leq b\), \(\gamma \geq \) 90°.