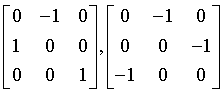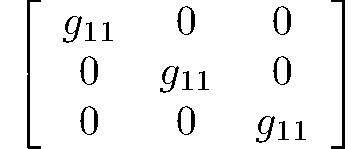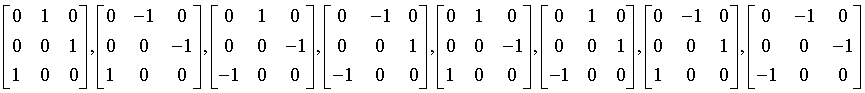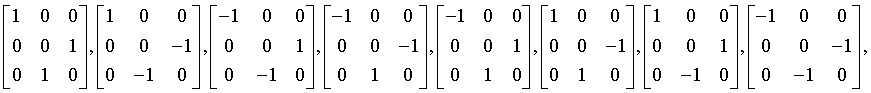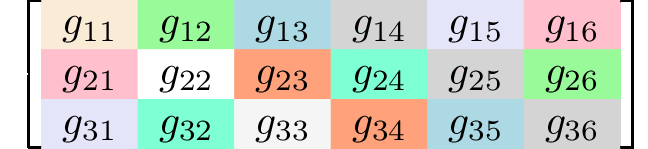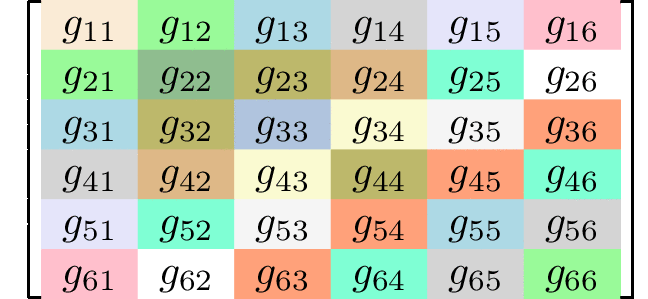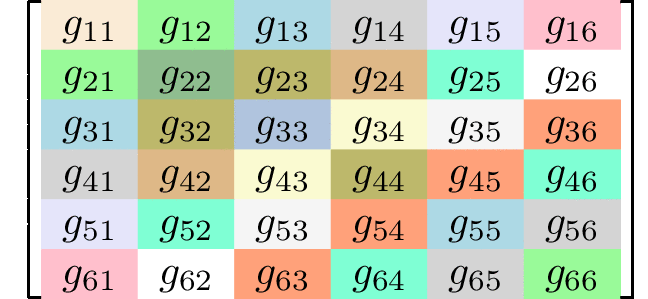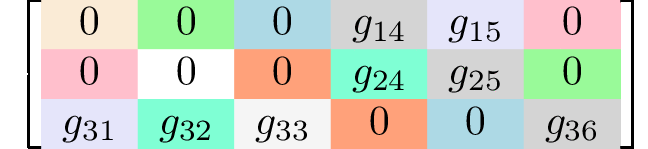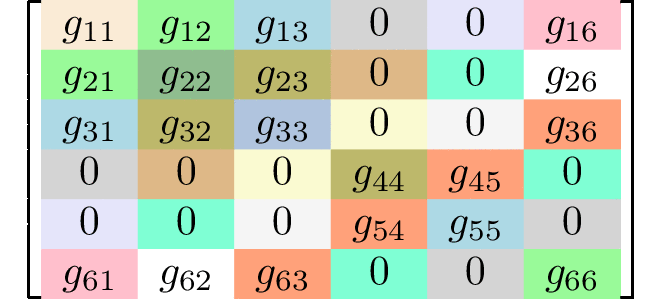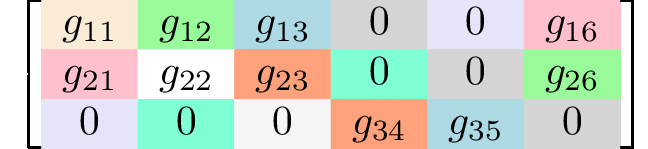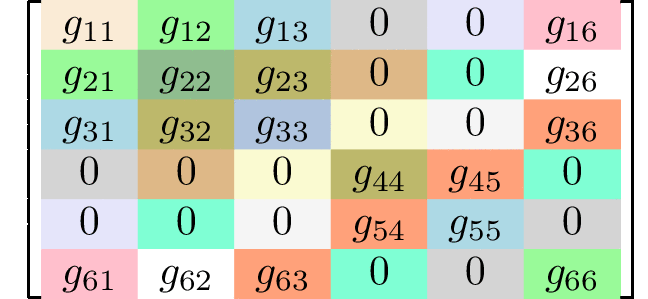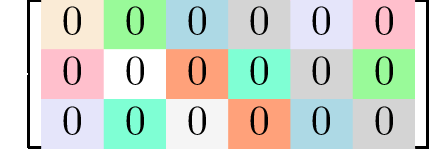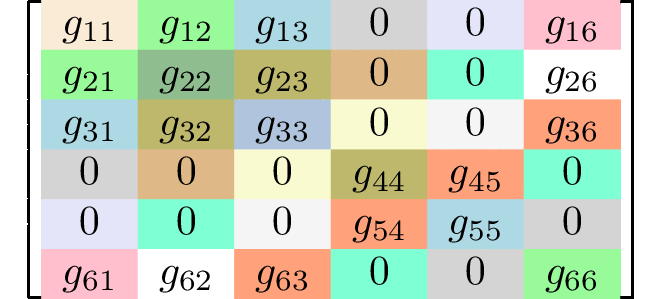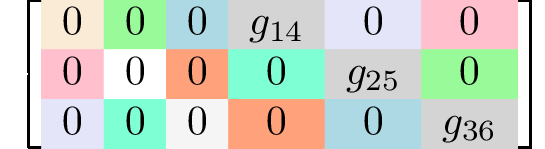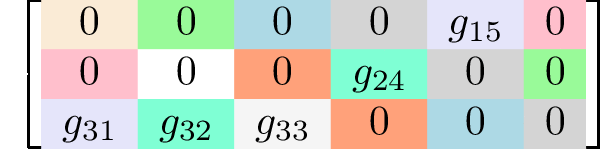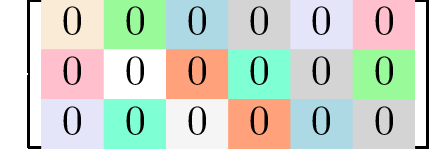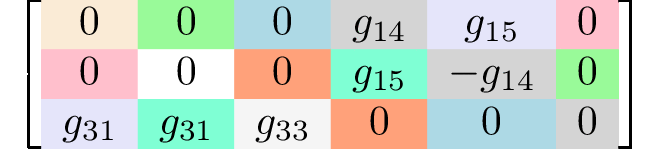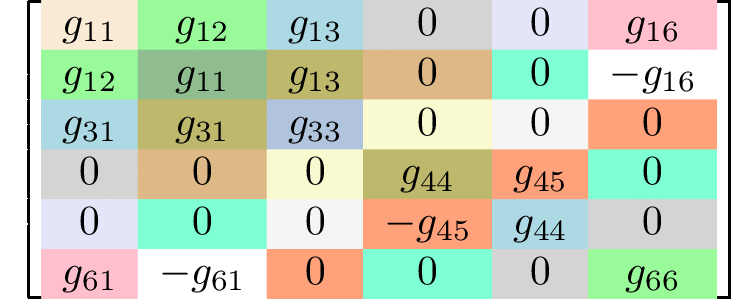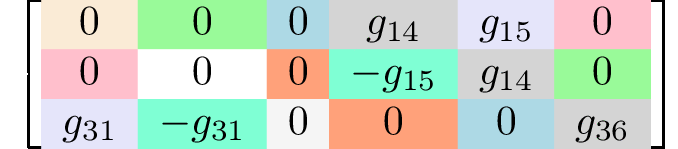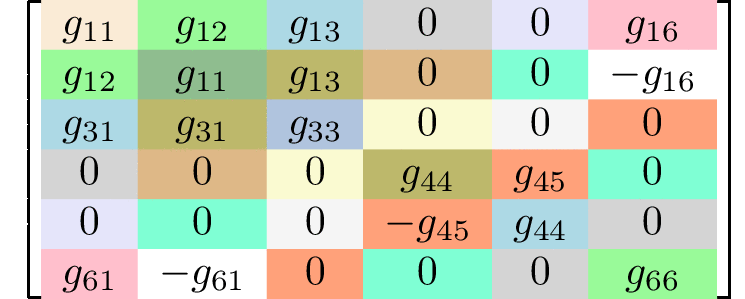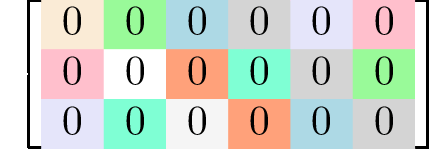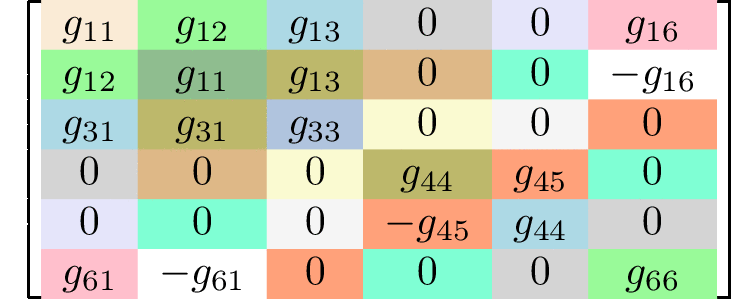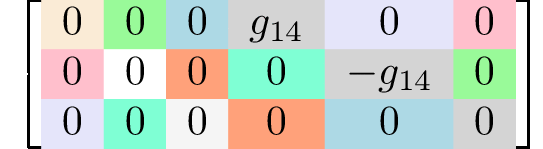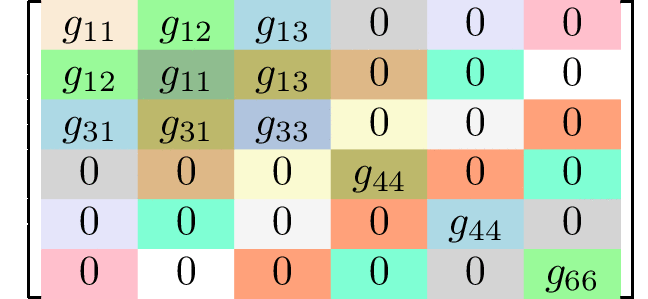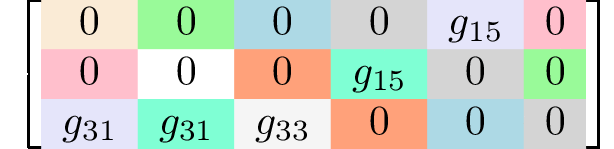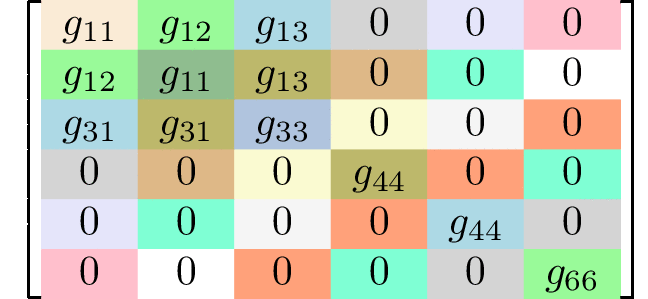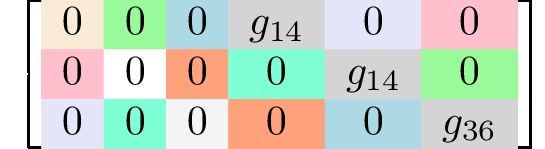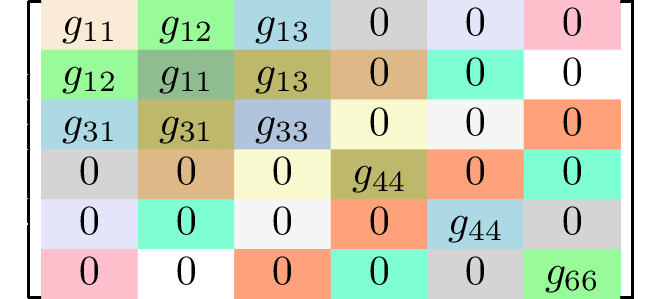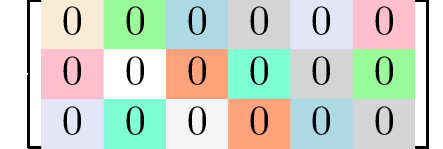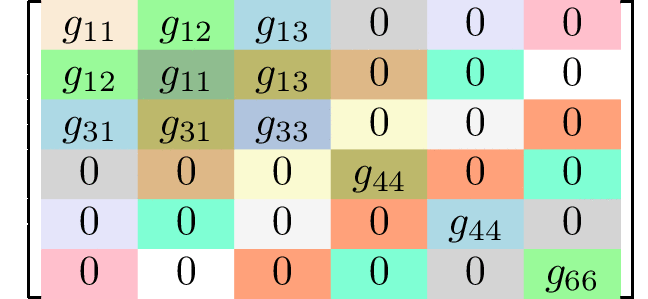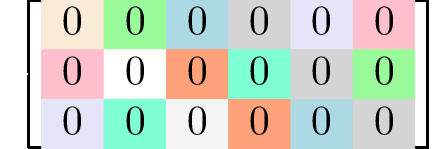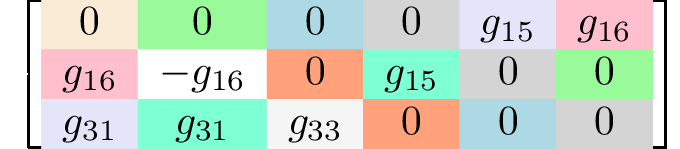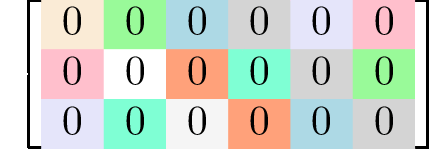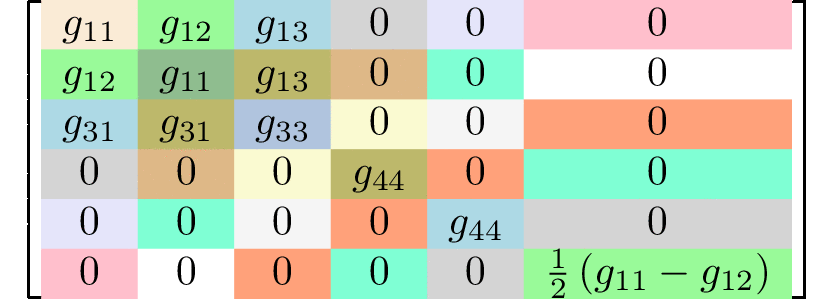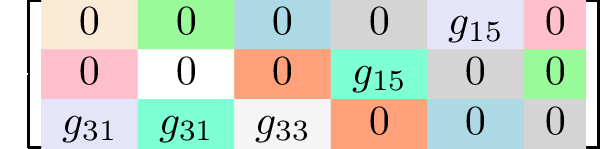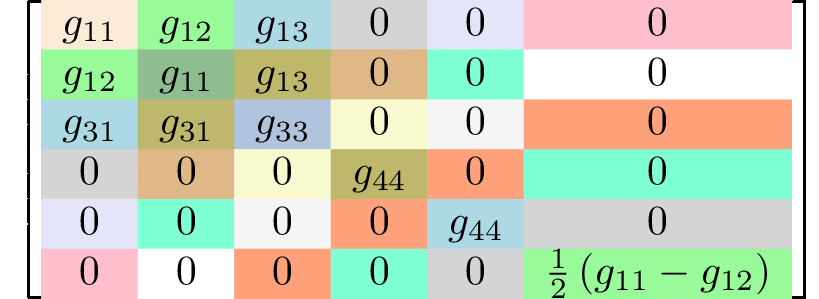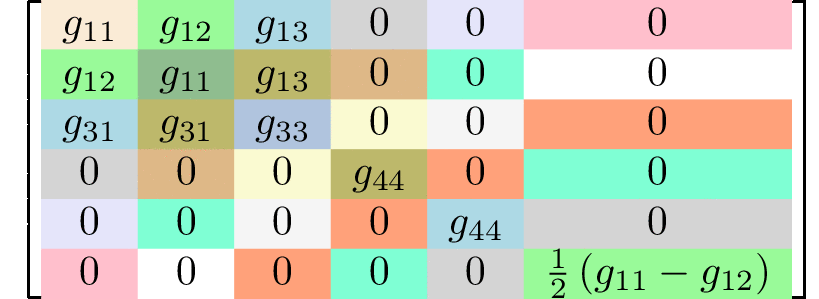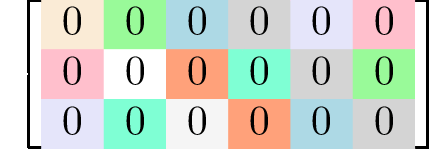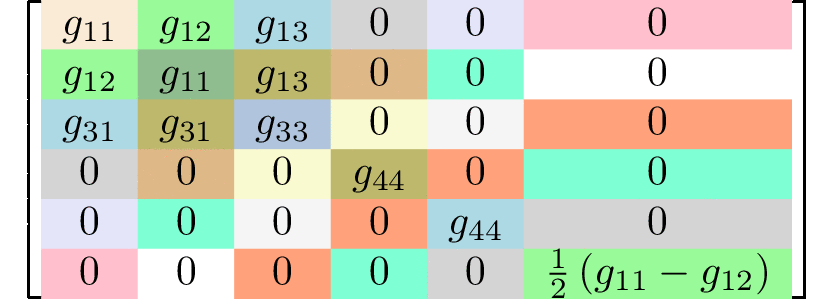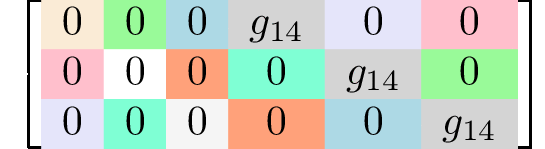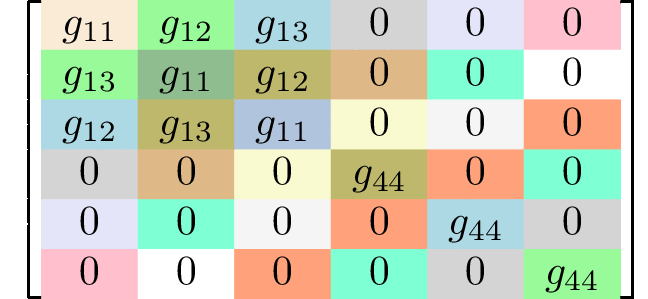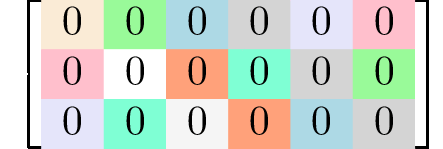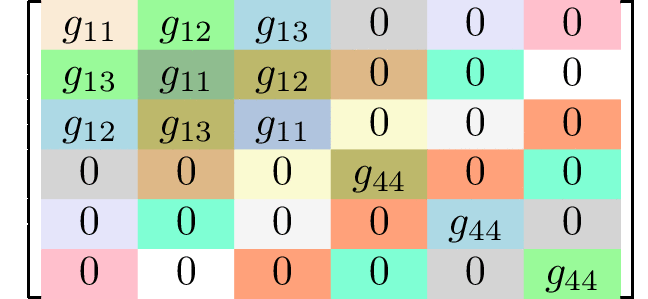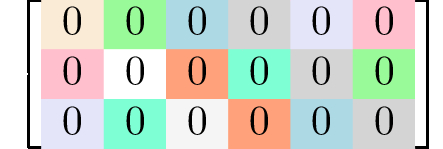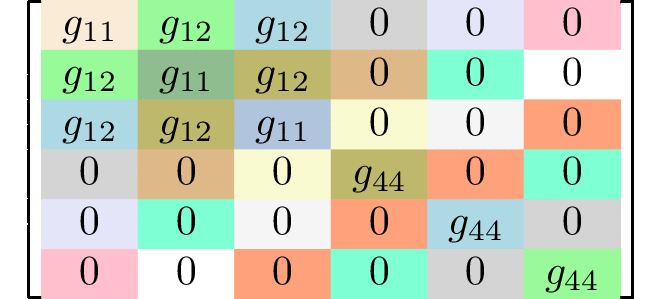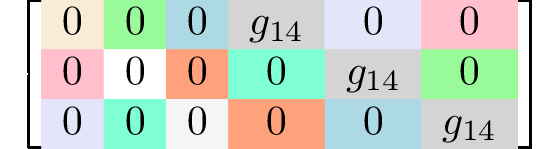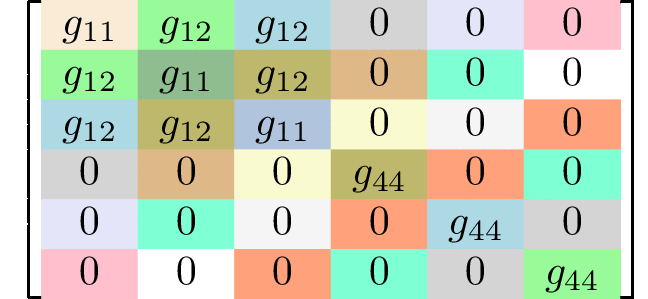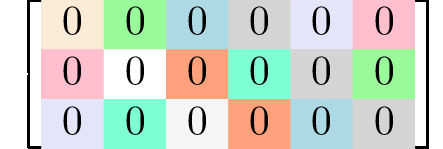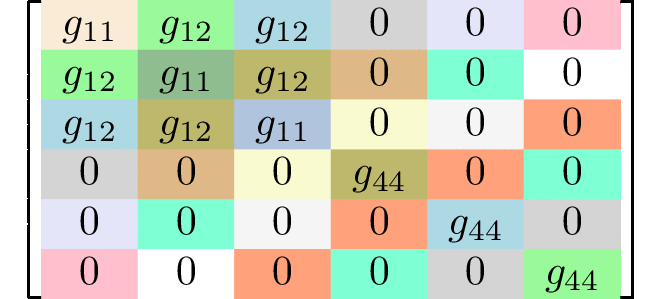The 32 Crystal Classes
Crystal system
Crystal Class
2-fold axes
3-fold axes
4-fold axes
6-fold axes
mirror planes
inversion
Examples
Number of symmetry elements
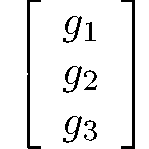
Generating matrices
rank 1 tensors1
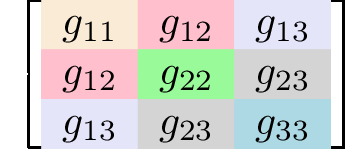
rank 2 symmetric tensors2
rank 2 asymmetric tensors
rank 3 tensors3
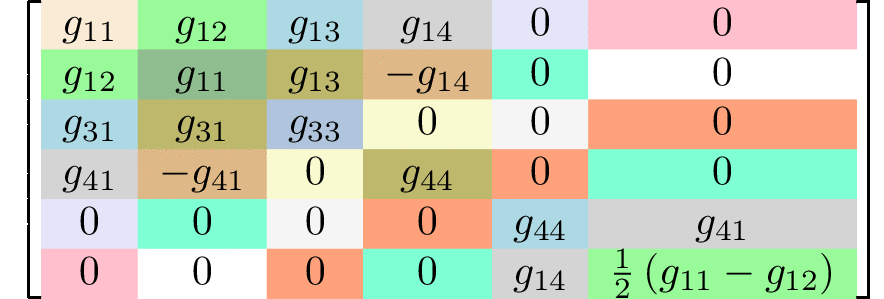
rank 4 tensors
Group elements
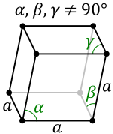
Triclinic
a ≠ b ≠ c
α ≠ β ≠ γ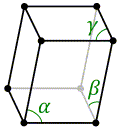
triclinic-pedial
1
C1
-
-
-
-
-
n
1
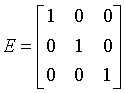
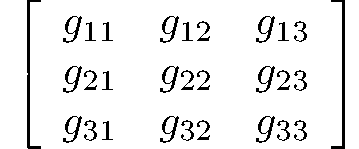
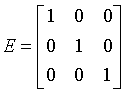
triclinic-pinacoidal
1
S2 = Ci
2: P1
-
-
-
-
-
y
2


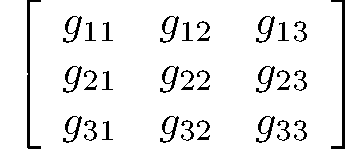
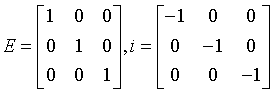
Monoclinic
a ≠ b ≠ c
α ≠ 90°, β = γ = 90°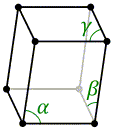
monoclinic-sphenoidal
2
C2
3: P2, 4: P21, 5: C2
1
-
-
-
-
n
4: sucrose
2
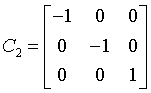
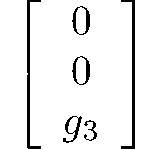

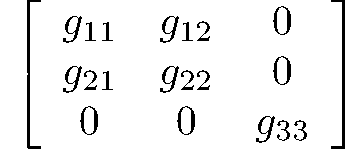

monoclinic-domatic
m
C1h = Cs
6: Pm, 7: Pc, 8: Cm, 9: Cc
-
-
-
-
1
n
2
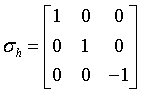
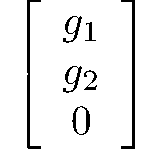
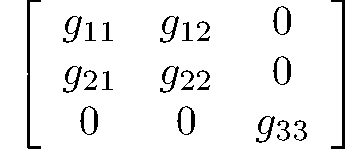
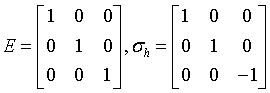
monoclinic-prismatic
$\frac{2}{m}$
C2h
10: P2/m, 11: P21/m, 12: C2/m, 13: P2/c, 14: P21/c, 15: C2/c
1
-
-
-
1
y
4
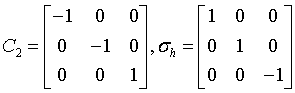

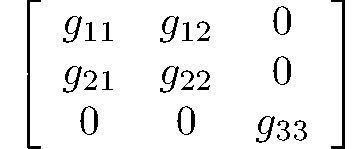
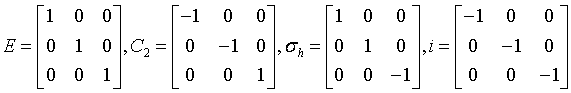
Crystal system
Crystal Class
2-fold axes
3-fold axes
4-fold axes
6-fold axes
mirror planes
inversion
Examples
Number of symmetry elements
Generating matrices
rank 1 tensors1
rank 2 symmetric tensors2
rank 2 asymmetric tensors
rank 3 tensors3
rank 4 tensors
Group elements
Orthorhombic
a ≠ b ≠ c
α = β = γ = 90°
orthorhombic-disphenoidal
222
V = D2
16: P222, 17: P2221, 18: P21212, 19: P212121, 20: C2221, 21: C222, 22: F222, 23: I222, 24: I212121
3
-
-
-
-
n
4
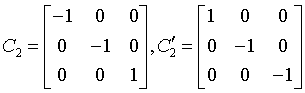

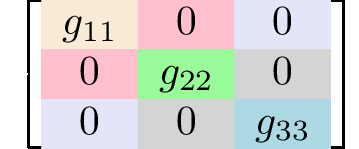
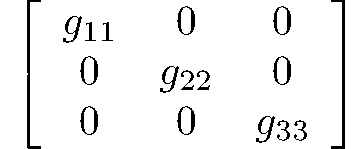

orthorhombic-pyramidal
mm2
C2v
25: Pmm2, 26: Pmc21, 27: Pcc2, 28: Pma2, 29: Pca21, 30: Pnc2, 31: Pmn21, 32: Pba2, 33: Pna21, 34: Pnn2 35: Cmm2, 36: Cmc21, 37: Ccc2, 38: Amm2, 39: Aem2, 40: Ama2, 41: Aea2, 42: Fmm2, 43: Fdd2, 44: Imm2, 45: Iba2, 46: Ima2
1
-
-
-
2
n
4
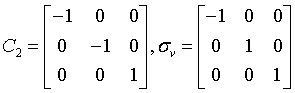
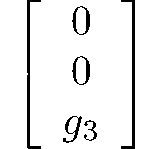
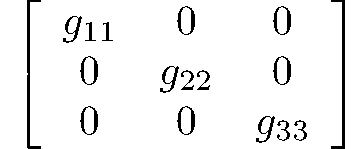
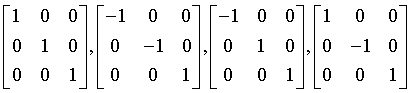
orthorhombic-dipyramidal
mmm
Vh = D2h
47: Pmmm, 48: Pnnn, 49: Pccm, 50: Pban, 51: Pmma, 52: Pnna, 53: Pmna, 54: Pcca, 55: Pbam, 56: Pccn, 57: Pbcm, 58: Pnnm, 59: Pmmn, 60: Pbcn, 61: Pbca, 62: Pnma 63: Cmcm, 64: Cmce, 65: Cmmm, 66: Cccm, 67: Cmme, 68: Ccce, 69: Fmmm, 70: Fddd, 71: Immm, 72: Ibam, 73: Ibca, 74: Imma
3
-
-
-
3
y
47: YBa2Cu3O7-x
62: Fe3C
64: αGa
70: αS
8


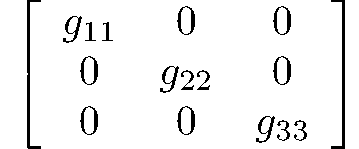
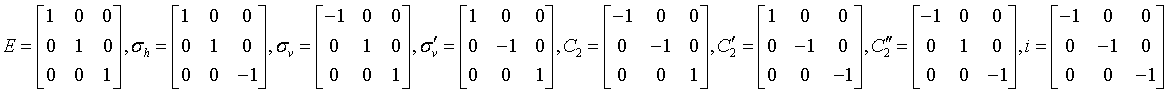
Crystal system
Crystal Class
2-fold axes
3-fold axes
4-fold axes
6-fold axes
mirror planes
inversion
Examples
Number of symmetry elements
Generating matrices
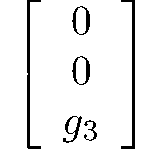
rank 1 tensors1
rank 2 symmetric tensors2
rank 2 asymmetric tensors
rank 3 tensors3
rank 4 tensors
Group elements
tetragonal-pyramidal
4
C4
75: P4, 76: P41, 77: P42, 78: P43, 79: I4, 80: I41
-
-
1
-
-
n
4
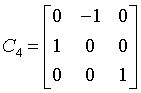
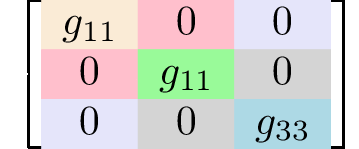
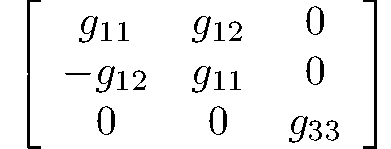
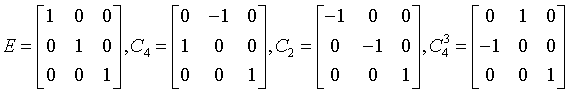
tetragonal-disphenoidal
4
S4
81: P4, 82: I4
1
-
-
-
-
n
4
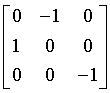

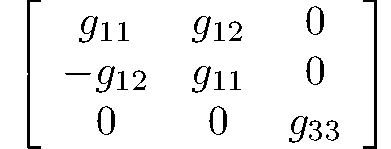
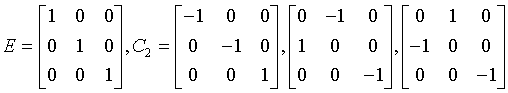
tetragonal-dipyramidal
$\frac{4}{m}$
C4h
83: P4/m, 84: P42/m, 85: P4/n, 86: P42/n, 87: I4/m, 88: I41/a
-
-
1
-
1
y
8
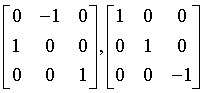

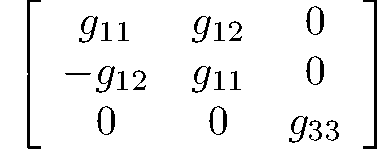
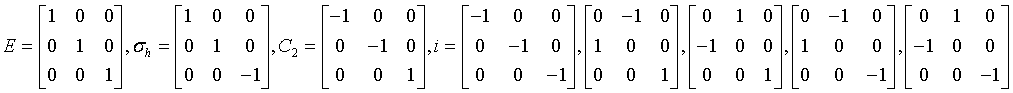
tetragonal-trapezoidal
422
D4
89: P422, 90: P4212, 91: P4122, 92: P41212, 93: P4222, 94: P42212, 95: P4322, 96: P43212, 97: I422, 98: I4122
4
-
1
-
-
n
8
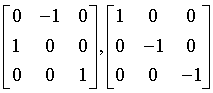

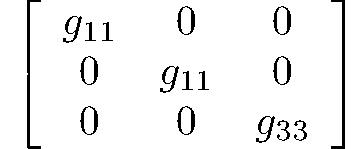

ditetragonal-pyramidal
4mm
C4v
99: P4mm, 100: P4bm, 101: P42cm, 102: P42nm, 103: P4cc, 104: P4nc, 105: P42mc, 106: P42bc, 107: I4mm, 108: I4cm, 109: I41md, 110: I41cd
-
-
-
-
4
n
99: PZT PbZrxTi1-xO3 x<0.52
8
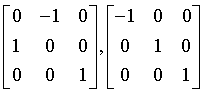
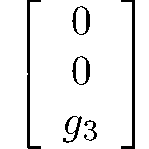
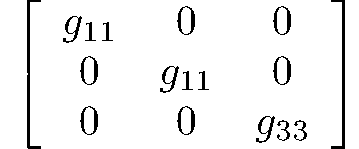
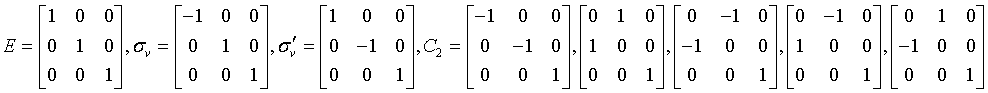
tetragonal-scalenoidal
42m
Vd = D2d
111: P42m, 112: P42c, 113: P421m, 114: P421c, 115: P4m2, 116: P4c2, 117: P4b2, 118: P4n2, 119: I4m2, 120: I4c2, 121: I42m, 122: I42d
3
-
-
-
2
n
8
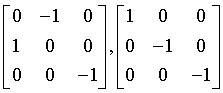

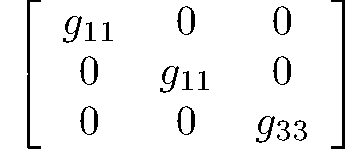

ditetragonal-dipyramidal
$\frac{4}{m}mm$
D4h
123: P4/mmm, 124: P4/mcc, 125: P4/nbm, 126: P4/nnc, 127: P4/mbm, 128: P4/mnc, 129: P4/nmm, 130: P4/ncc, 131: P42/mmc, 132: P42/mcm, 133: P42/nbc, 134: P42/nnm, 135: P42/mbc, 136: P42/mnm, 137: P42/nmc, 138: P42/ncm, 139: I4/mmm, 140: I4/mcm, 141: I41/amd, 142: I41/acd
4
-
1
-
5
y
123: Tetrataenite, 139: In
141: βSn
16
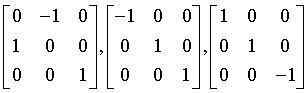


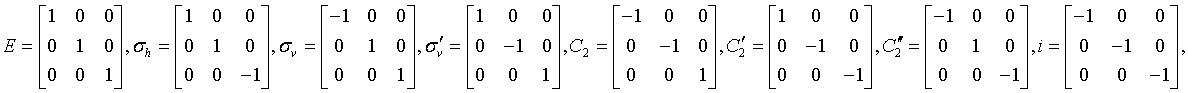
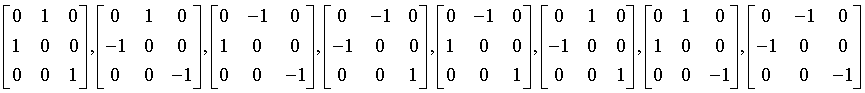
Crystal system
Crystal Class
2-fold axes
3-fold axes
4-fold axes
6-fold axes
mirror planes
inversion
Examples
Number of symmetry elements
Generating matrices
rank 1 tensors1
rank 2 symmetric tensors2
rank 2 asymmetric tensors
rank 3 tensors3
rank 4 tensors
Group elements
trigonal-pyramidal
3
C3
143: P3, 144: P31, 145: P32, 146: R3
-
1
-
-
-
n
3
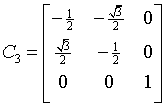
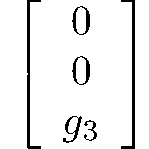
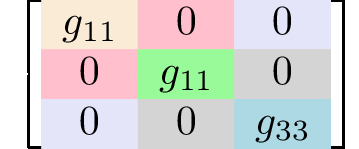
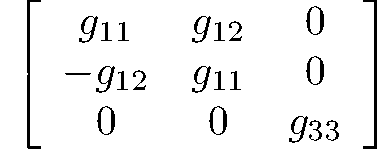
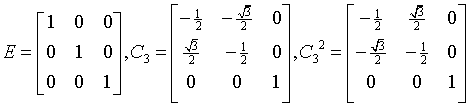
rhombohedral
3
S6 = C6i
147: P3, 148: R3
-
1
-
-
-
y
6


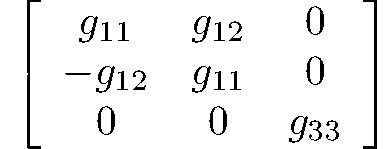
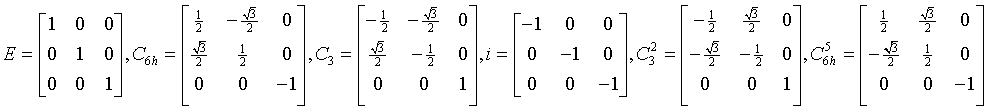
trigonal-trapezoidal
32
D3
149: P312, 150: P321, 151: P3112, 152: P3121, 153: P3212, 154: P3221, 155: R32
3
1
-
-
-
n
154: α-Quartz
6


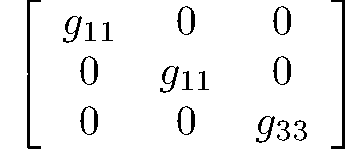
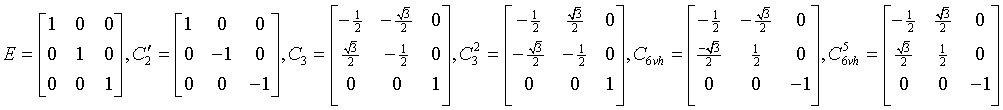
ditrigonal-pyramidal
3m
C3v
156: P3m1, 157: P31m, 158: P3c1, 159: P31c, 160: R3m, 161: R3c
-
1
-
-
3
n
161: ferroelectric LiNbO3
6
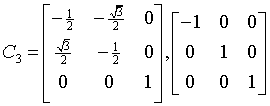

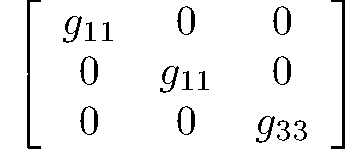
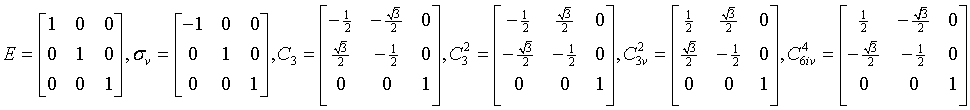
ditrigonal-scalahedral
3m
D3d
162: P31m, 163: P31c, 164: P3m1, 165: P3c1, 166: R3m, 167: R3c
3
1
-
-
3
y
167: calcite, paraelectric LiNbO3, sapphire (α-Al2O3)
12
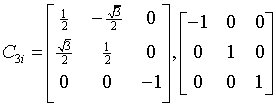

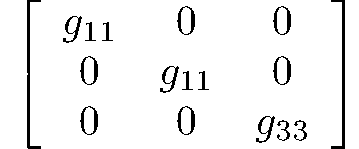
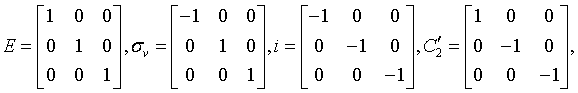
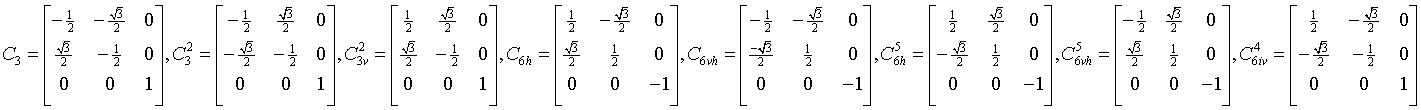
Crystal system
Crystal Class
2-fold axes
3-fold axes
4-fold axes
6-fold axes
mirror planes
inversion
Examples
Number of symmetry elements
Generating matrices
rank 1 tensors1
rank 2 symmetric tensors2
rank 2 asymmetric tensors
rank 3 tensors3
rank 4 tensors
Group elements
hexagonal-pyramidal
6
C6
168: P6, 169: P61, 170: P65, 171: P62, 172: P64, 173: P63
-
-
-
1
-
n
6
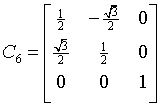
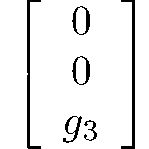
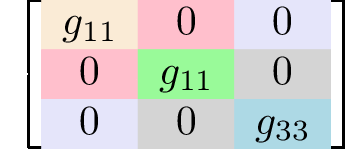
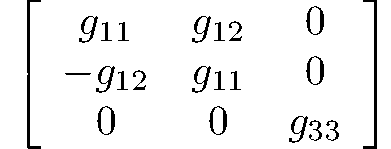
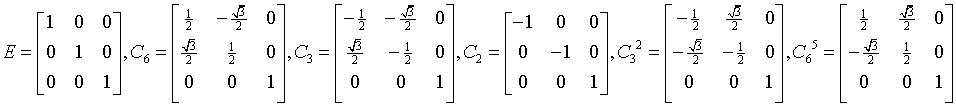
trigonal-dipyramidal
6
C3h = S3
174: P6
-
1
-
-
1
n
6
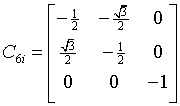

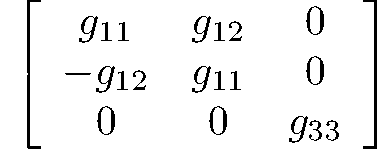
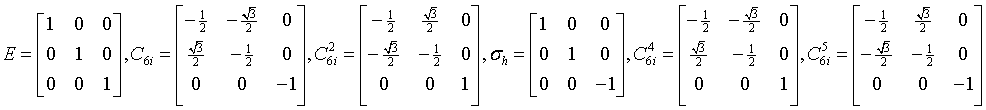
hexagonal-dipyramidal
$\frac{6}{m}$
C6h
175: P6/m, 176: P63/m
-
-
-
1
1
y
12
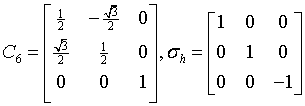

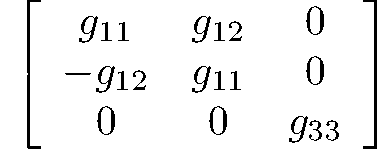
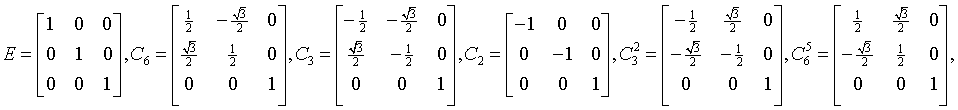
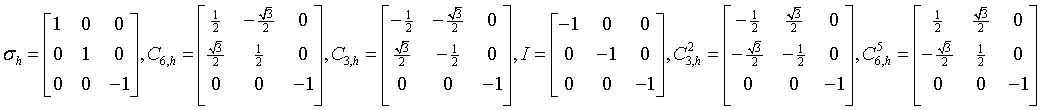
hexagonal-trapezoidal
622
D6
177: P622, 178: P6122, 179: P6522, 180: P6222, 181: P6422, 182: P6322
6
-
-
1
-
n
180: β-Quartz
12
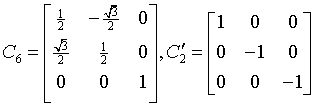

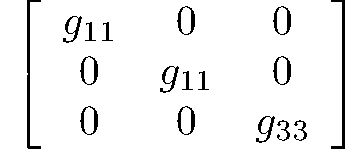

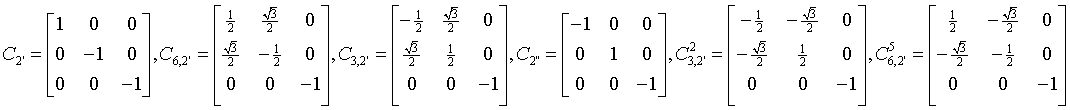
dihexagonal-pyramidals
6mm
C6v
183: P6mm, 184: P6cc, 185: P63cm, 186: P63mc
-
-
-
1
6
n
186: Wurtzite,
12
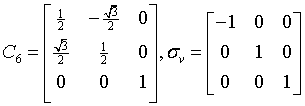
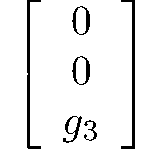
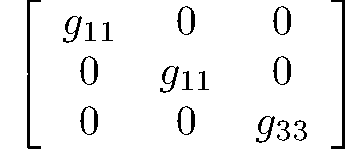
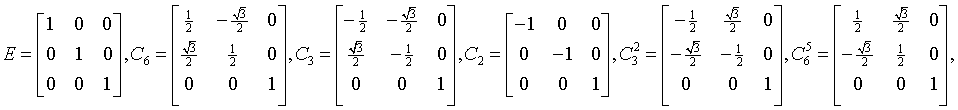
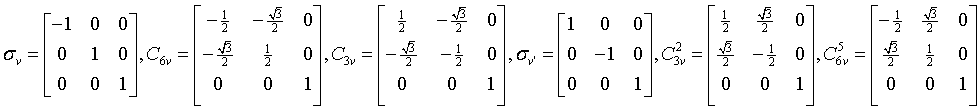
ditrigonal-dipyramidal
6m2
D3h
187: P6m2, 188: P6c2, 189: P62m, 190: P62c
3
1
-s
-
4
n
12
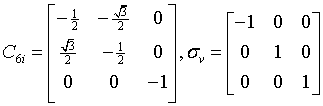

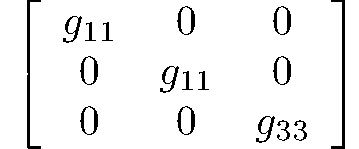
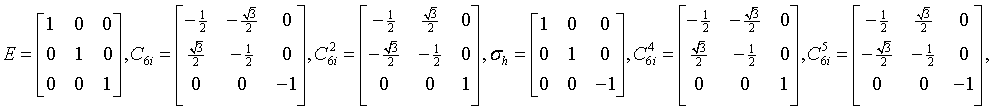
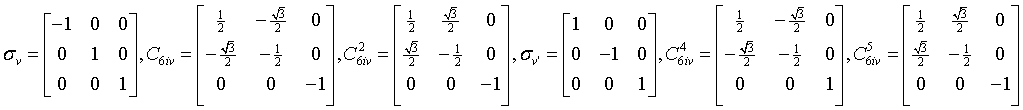
dihexagonal-dipyramidal
$\frac{6}{m}mm$
D6h
191: P6/mmm, 192: P6/mcc, 193: P63/mcm, 194: P63/mmc
6
-
-
1
7
y
194: hcp, Mg, Be, Sc, α-Ti, Co, Zn, Y, Zr, Tc, Ru, Cd, Gd, Tb, Dy, Ho, Er, Tm, Lu, Hf, Re, Os, Tl, graphite, MoS2, ice Ih
24
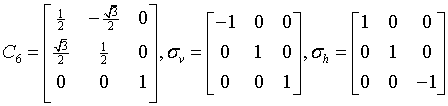


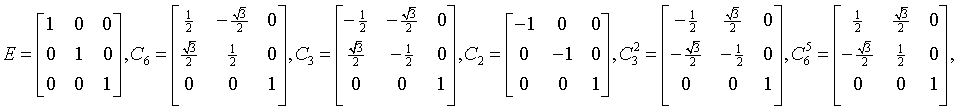
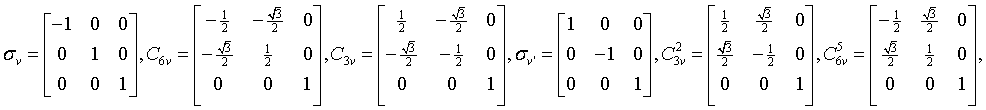
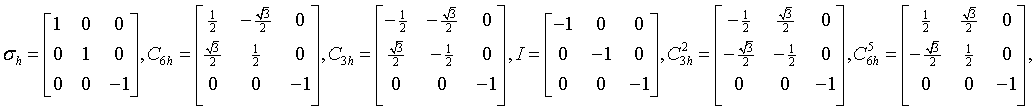
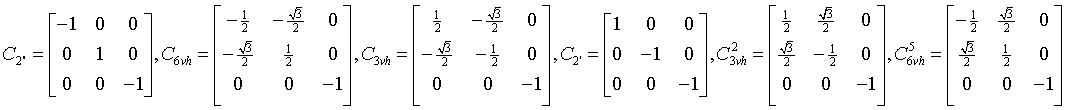
Crystal system
Crystal Class
2-fold axes
3-fold axes
4-fold axes
6-fold axes
mirror planes
inversion
Examples
Number of symmetry elements
Generating matrices
rank 1 tensors1
rank 2 symmetric tensors2
rank 2 asymmetric tensors
rank 3 tensors3
rank 4 tensors
Group elements
tetrahedral
23
T
195: P23, 196: F23, 197: I23, 198: P213, 199: I213
3
4
-
-
-
n
12
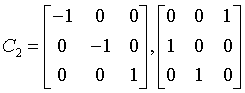

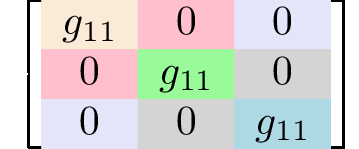
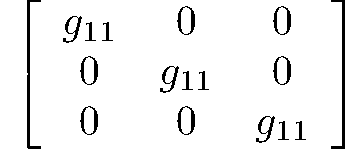
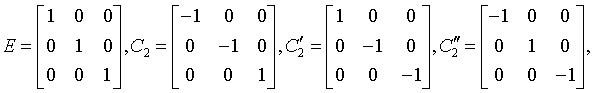
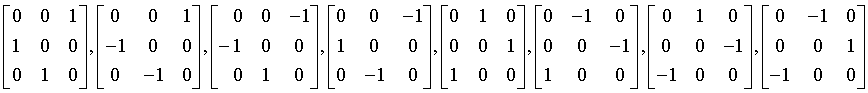
diploidal
m3
Th
200: Pm3, 201: Pn3, 202: Fm3, 203: Fd3, 204: Im3, 205: Pa3, 206: Ia3
3
4
-
-
3
y
24
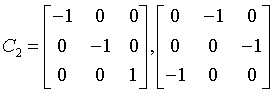


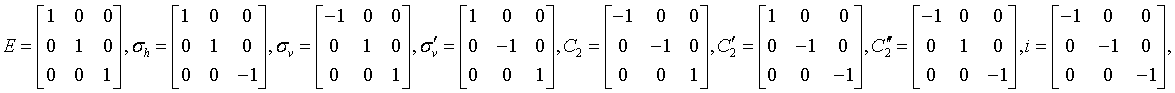
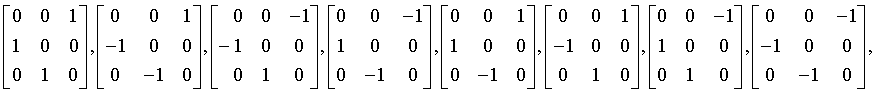
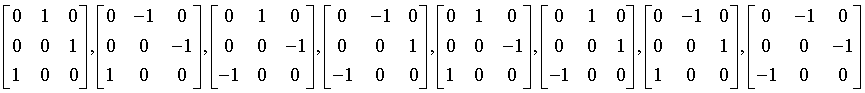
gyroidal
432
O
207: P432, 208: P4232, 209: F432, 210: F4132, 211: I432, 212: P4332, 213: P4132, 214: I4132
6
4
3
-
-
n
24
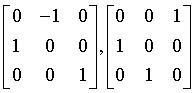

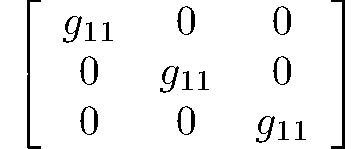
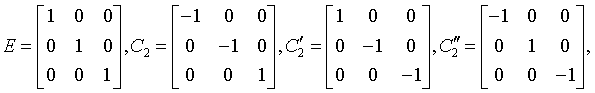
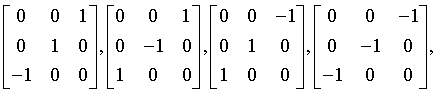
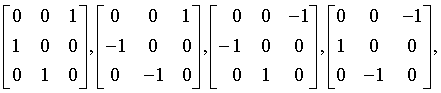
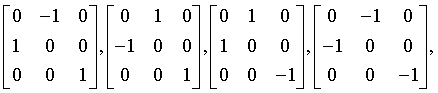
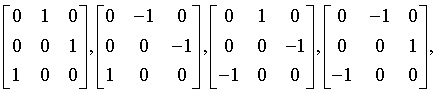
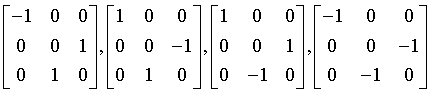
hextetrahedral
43m
Td
215: P43m, 216: F43m, 217: I43m, 218: P43n, 219: F43c, 220: I43d
3
4
-
-
6
n
216: Zincblende, GaAs, GaP, InAs, SiC
24
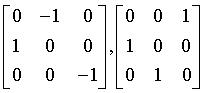

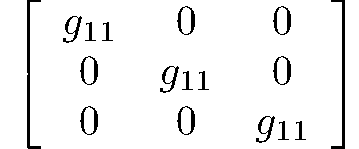
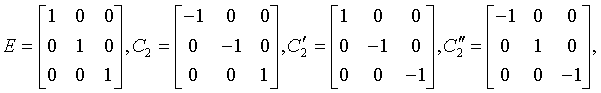
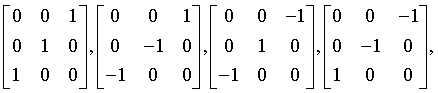
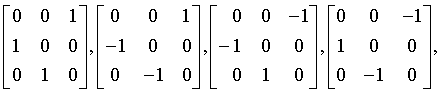
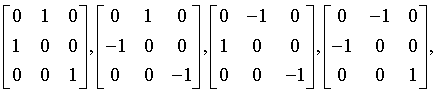
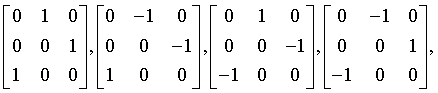
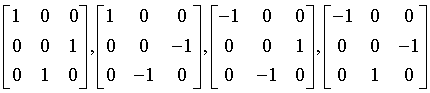
hexoctahedral
m3m
Oh
221: Pm3m, 222: Pn3n, 223: Pm3n, 224: Pn3m 225: Fm3m, 226: Fm3c, 227: Fd3m, 228: Fd3c 229: Im3m, 230: Ia3d
6
4
3
-
9
y
221: CsCl, cubic perovskite
225: fcc, Al, Cu, Ni, Ag, Pt, Au, Pb, γ-Fe, NaCl
227: diamond, C, Si, Ge, α-Sn, spinel
229: bcc, Na, K, Cr, α-Fe, β-Ti, Nb, Mo, Ta
48