Reelle und virtuelle Bilder

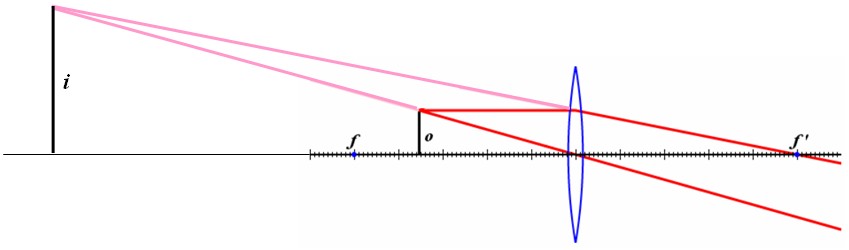
Ein Objekt $o$ befindet sich im Abstand $x_o$ vor einer dünnen Linse. Das Bild $i$ dieses Objekts erscheint im Abstand $x_i$ hinter der Linse. Es gibt drei ausgezeichnete Strahlen, welche für das Auffinden der Bildposition benutzt werden können. Der Strahl, welcher das Objekt verlässt und parallel zur optischen Achse verläuft, wird durch die Linse in den Brennpunkt, der sich hinter der Linse befindet, gebrochen. Ein Strahl, der vom Objekt ausgehend den objektseitigen Brennpunkt schneidet, läuft nach Brechung an der Linse parallel zur optischen Achse. Der vom Objekt ausgehende Strahl durch den Linsenmittelpunkt wird nicht gebrochen. Diese drei Strahlen (in rot dargestellt) schneiden sich am Bild. Die Abbildungsgleichung kann benutzt werden, um die Entfernung der Linse zum Objekt $x_o$ und zum Bild $x_i$ in Beziehung zur Brennweite $f$ zu setzen. Wenn die Position der Linse ist $ x = 0 $ und $ x_o < 0 $, ist die Abbildungsgleichung,

$\Large \frac{-1}{x_o}+\frac{1}{x_i}= \frac{1}{f}$.

Ein Objekt, welches weiter von einer Sammellinse entfernt ist als die Brennweite, wird auf die andere Linsenseite abgebildet. Wird ein Schirm an diese Bildposition eingebracht, ist das Objekt scharf zu erkennen, erscheint jedoch umgekehrt. Dies ist ein reelles, umgekehrtes Bild. Die Vergrößerung ergibt sich aus Höhe des Bildes dividiert durch die Höhe des Objekts. Mit etwas Trigonometrie bzw. dem Strahlensatz erhält man die Vergrößerung, $m=y_i/y_o=f/(x_o+f)$. Eine negative Vergrößerung bedeutet das Vorliegen eines umgekehrten Bildes.

Steht ein Objekt näher zu einer Sammellinse als die Brennweite, laufen die Strahlen auf der anderen Seite der Linse auseinander (divergieren). Durch Rückextrapolieren dieser Linien (pink) kann die Position des virtuellen Bildes gefunden werden. Auf der gegenüberliegenden Seite scheint es, als ob das Licht vom virtuellen Bild kommen würde. Versucht man jedoch eine Kamera an die Position des virtuellen Bildes einzubringen, ist es nicht möglich, das Bild aufzunehmen. Das virtuelle Bild ist aufrecht und die Vergrößerung ist positiv.

Die Brennweite ist für eine Sammellinse positiv und für eine Zerstreuungslinse negativ. Zerstreuungslinsen liefern stets virtuelle, aufrechte Bilder.

Lupe
Ein Person kann nicht auf ein Objekt fokusieren, wenn es zu nah ist. Die minimale benötigte Entfernung, bei der das Auge auf ein Objekt fokusieren kann, heißt Nahpunkt. Diese Entfernung hängt von der Person ab, ist jedoch typischerweise ca. 25 cm. Wird das Objekt in die Brennweite in unmittelbarer Nähe des Brennpunktes einer Sammellinse gebracht, werden die divergierenden Strahlen in einen paralleleren Verlauf gebrochen. So ist es möglich, auf das Objekt zu fokusieren, obwohl es näher als der Nahpunkt ist.