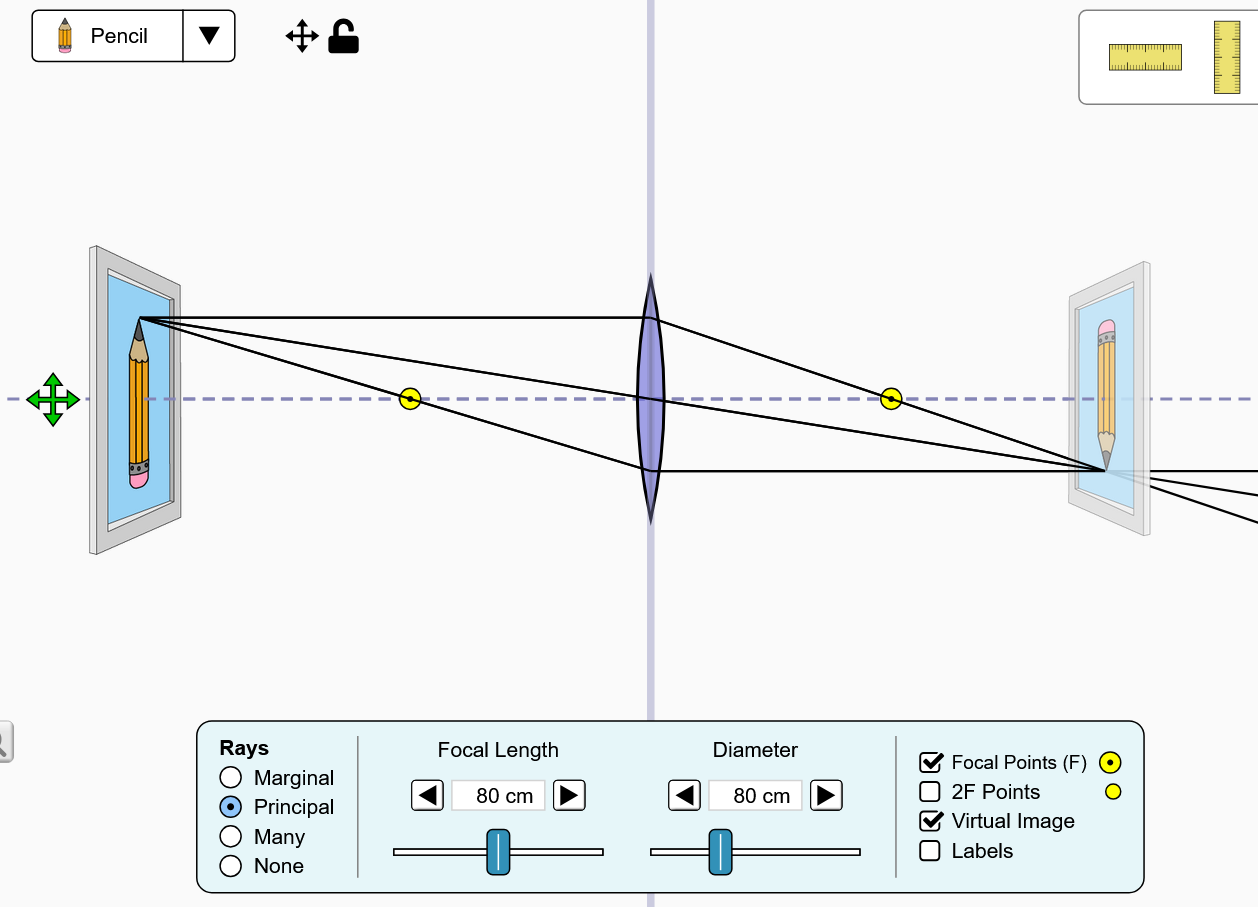
Abbildungsgleichung der dünne Linse

$f=$

[cm]

$x_o=$

[cm]

$y_o=$

[cm]

$x_i=$

[cm]  $D=$ [m-1]

$y_i=$

[cm] $m=$

Your browser does not support the canvas element.

Die Abbildungsgleichung der dünnen Linse kann mithilfe der roten Dreiecke im Bild hergeleitet werden. Da die Dreiecke die gleichen Winkel besitzen, gilt

$$m=\frac{x_i}{x_o}=\frac{y_i}{y_o}=-\frac{x_i-f}{f}.$$

Hier ist $m$ die Vergrößerung. Es werden beide Seiten auf einen gemeinsamen Nenner gebracht,

$$\frac{x_if}{x_of}=-\frac{x_ix_o-x_of}{x_of}.$$

Beide Seiten werden durch $x_i$ geteilt,

$$\frac{x_if}{x_ox_if}=-\frac{x_ix_o-x_of}{x_ox_if}$$

und vereinfacht,

$$\frac{1}{x_o}=-\frac{1}{f}+\frac{1}{x_i}.$$

Umarrangiert erhält man,


$\hspace{0.5cm}\Large -\frac{1}{x_o}+\frac{1}{x_i}=\frac{1}{f}.\hspace{0.5cm}$

Dies ist die bekannte Abbildungsgleichung dünner Linsen. Da das Objekt sich links der Linse befindet, ist $x_o$ eine negative Zahl. Diese Ableitung nahm an, dass sich die Linse an der Position $x = 0$ befindet. Dies ist unpraktisch, wenn ein optisches System mehr Linsen enthält. Wenn die Position der Linse $x_{\text{lens}}$ ist, lautet die Abbildungsgleichung dünner Linsen:

$$\frac{1}{x_{\text{lens}}-x_o}+\frac{1}{x_i -x_{\text{lens}}}=\frac{1}{f}.$$

Beachten Sie, dass sich das Bild in der Simulation mitbewegt, wenn Sie das Objekt bewegen.