Dicke Linsen

Wir betrachten eine Linse, die aus zwei sphärischen Oberflächen besteht, die auf einer optischen Achse zentriert sind, und einer zylindrischen Oberfläche, bei der die Mittelachse des Zylinders entlang der optischen Achse verläuft. Die linke sphärische Grenzfläche schneidet die optische Achse bei $-d_1$ und hat einen Radius $R_1$. Die rechte sphärische Grenzfläche schneidet die optische Achse bei $d_2$ und hat einen Radius $R_2$.

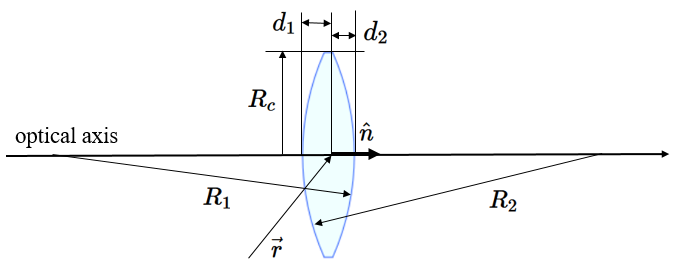
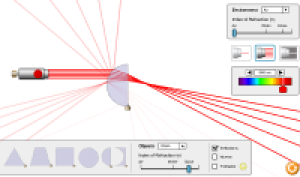
Der Radius des Zylinders beträgt $R_c$. Die entlang der optischen Achse gemessene Dicke der Linse beträgt $d_1 + d_2$. Die unten gezeigte Ansicht zeigt nach unten auf die $x-y$-Ebene. Es ist möglich, die optische Achse der Linse um einen Winkel $\phi$ gegenüber der $x-$Achse zu drehen. Lichtstrahlen verlassen ein Objekt $(x_o,y_o)$ und werden an den Grenzflächen reflektiert und gebrochen. Die reflektierten Strahlen haben 1/10 der Intensität der einfallenden Strahlen und die gebrochenen Strahlen haben 9/10 der Intensität der einfallenden Strahlen. Die Brechung kann mithilfe des Snelliusschen Brechungsgesetzes an einer sphärischen Grenzfläche berechnet werden. Der Brechungsindex ist wellenlängenabhängig und wird durch ein Cauchy-Gesetz $n = A + B/\lambda^2$ modelliert. Die von den Lichtquellen verwendeten Wellenlängen werden in Nanometern als Liste in eckigen Klammern angegeben, z. B. [450,510,650].

Linsentypen:

Eine dreidimensionale Version dieser App ist hier verfügbar.