Doppelspaltexperiment
|
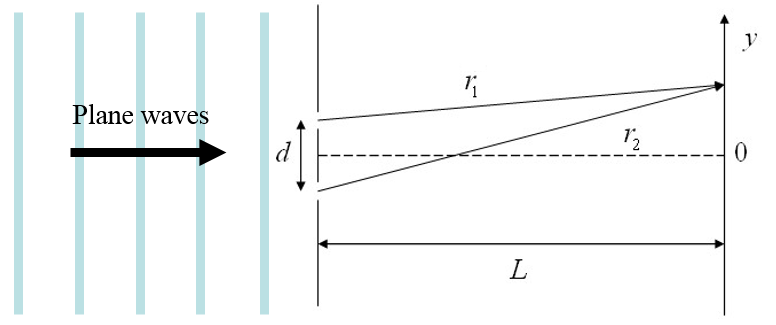
In einem Doppelspaltexperiment fallen die Lichtwellen durch zwei schmale Schlitze, welche den Abstand $d$ haben. Das Interferenzmuster wird auf einem Schirm beobachtet, welcher den Abstand $L$ von den Spalten hat.
Die kleine Teilung des rechten Maßstabes ist in mm. |
Hier ist $r_1$ der Abstand zwischen Quelle 1 und $r_2$ der Abstand von Quelle 2. Die Wellenzahl $k$ hängt mit der Wellenlänge zusammen $\lambda$, $k=\frac{2\pi}{\lambda}$ und die Kreisfrequenz $\omega$ mit der Periodendauer $T$, $\omega=\frac{2\pi}{T}$.
Der jeweiligen Abstände von den beiden Quellen zu einem Punkt der Höhe $y$ auf den Schirm lauten:
$r_1 = \sqrt{L^2+(y-d/2)^2},$
$r_2 = \sqrt{L^2+(y+d/2)^2}.$
Die Wellen verlassen die Spalten mit der gleichen Amplitude $A$ und der gleichen Phase (die wir Null wählen). Die Wellen interferieren am Schirm. Die Amplitude der Wellen am Schirm ist:
$\frac{A}{\sqrt{r_1}} \exp (ikr_1)+\frac{A}{\sqrt{r_2}} \exp (ikr_2).$
Die Intensität ist das Quadrat der Amplitude
$\large I \propto \left(\frac{A}{\sqrt{r_1}} \cos(kr_1)+\frac{A}{\sqrt{r_2}} \cos(kr_2)\right)^2+\left(\frac{A}{\sqrt{r_1}} \sin(kr_1)+\frac{A}{\sqrt{r_2}} \sin(kr_2 )\right)^2.$
Dies ist das exakte Resultat für das Interferenzmuster. Mit einer Näherung kann es jedoch in einer einfacheren Form beschrieben werden. Für $y < < L$, $A/\sqrt{r_1} \approx A/\sqrt{r_2} \approx A/\sqrt{L}$. Unter Benutzung der trigonometrischen Beziehungen $\sin a+\sin b=2\sin ((a+b)/2)\cos ((a-b)/2)$ und $\cos a+\cos b=2\cos ((a+b)/2)\cos ((a-b)/2)$
$\large I \propto \frac{4A^2}{L} \left(\sin^2((kr_1+kr_2)/2)+\cos^2((kr_1+kr_2)/2)\right)\cos^2((kr_1-kr_2)/2).$
$\large I \propto \frac{4A^2}{L} \cos^2\left( \frac{kr_1-kr_2}{2}\right).$
$\large I \propto \frac{4A^2}{L} \cos^2\left( \frac{kdy}{2L}\right).$
| $\frac{I}{I_0}$ | |
$y$ |
Fernfeld
Im Fernfeld, d.h. wenn $L > > \lambda$ und $L > > y$, entsteht konstruktive Interferenz für $n\lambda=yd/L$ mit ganzzahligem $n$. Destruktive Interferenz wird für $(n+1/2)\lambda=yd/L$ beobachtet.