The Kronig-Penney model [1] is a simplified model for an electron in a one-dimensional periodic potential. The possible states that the electron can occupy are determined by the Schrödinger equation,

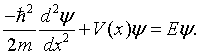
In the case of the Kroning-Penney model, the potential V(x) is a periodic square wave.

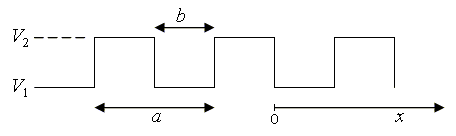
A virtue of this model is that it is possible to analytically determine the energy eigenvalues and eigenfunctions. It is also possible to find analytic expressions for the dispersion relation (E vs. k) and the electron density of states. [2] Derivations are given below.

This form can be used to plot the dispersion relation and the density of states for the Kronig Penney model.

V(x) [eV]  x [nm] Initial energy E1 =   [eV]  Final energy E2 =   [eV]  Number of energy points N  =   [eV]  Mass m =   [kg]  a  =   [m]  b  =   [m]  V1  =   [eV]  V2  =   [eV]  E [eV] ka D(E) [eV-1 nm-1] Data:

 

Solution of the Schrödinger equation for the Kronig-Penney potential

Since the Kronig-Penney potential exhibits translational symmetry, the energy eigenfunctions of the Schrödinger equation will simultaneously be eigenfunctions of the translation operator. As we often do in solid state physics, we proceed by seeking the eigenfunctions of the translation operator. The translation operator T shifts the solutions by one period, Tψ(x) = ψ(x + a). Notice that any function of the form,

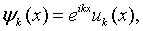
is an eigenfunction of the translation operator with eigenvalue e^ika.

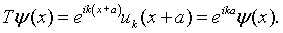
In solid state physics, functions like this are said to have Bloch form. The convention for describing electron waves in a periodic medium is to express them in terms of the eigenfunctions of the translation operator. These eigenfunctions have a well defined frequency and form a complete set that can be used to describe any wave. An eigenfunction is specified by the k that appears in the expression for the eigenvalue. It turns out that the physical interpretation of k is nearly the same as the wave number of harmonic waves (usually also called k).

The eigenfunctions of the translation operator can be readily constructed from any two linearly independent solutions of the one-dimensional Schrödinger equation. A convenient choice is,

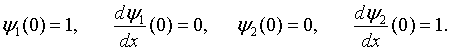
The solutions in region 1 (0 < x < b) are,

while the solutions in region 2 (b < x < a) are,

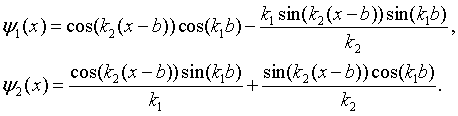
Here

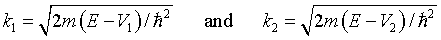
For energies where k₁ or k₂ are imaginary, the solutions are still real since cos(iθ) = cosh(θ) and sin(iθ) = isinh(θ).

Any other solution can be written as a linear combination of ψ₁(x) and ψ₂(x). In particular, ψ₁(x + a) and ψ₂(x + a) can be written in terms of ψ₁(x) and ψ₂(x). These solutions are related to each other by the matrix representation of the translation operator. [3]

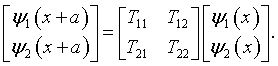
The elements of the translation matrix can be determined by evaluating the equation above and its derivative at x = 0.

The eigenfunctions and eigenvalues λ of this 2 × 2 matrix are easily determined to be,

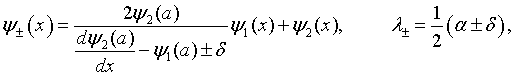
where

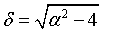
and

If periodic boundary conditions are used for a potential with N unit cells, then applying the translation operator N times brings the function back to its original position,

The eigenvalues of the translation operator are therefore the solutions to the equation λ^N = 1. These solutions are,

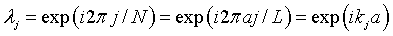
where j is an integer between -N/2 and N/2, L = Na is the length of the crystal, and k_j = 2πj/L are the allowed k values in the first Brillouin zone. The dispersion relation can be determined by first calculating α for a specific energy, solving for the eigenvalues λ and then solving the equation above for the wavenumber k,

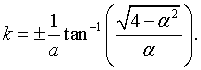
Whether the eigenvalues are real or imaginary depends on the magnitude of α. If α² > 4, the eigenvalues will be real and the solutions fall in a forbidden energy gap. If α² < 4, the eigenvalues will be a complex conjugate pair λ₊ = e^ika and λ_- = e^-ika.

The dispersion relation can be used to determine the density of states which is needed to calculate the thermodynamic properties of a system of noninteracting electrons. The one-dimensional density of states in k is D(k) = 2/π and thus the density of states in energy is,

where

and

---

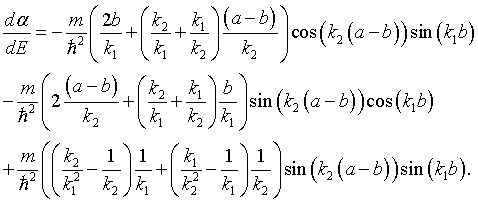
[1] R. de L. Kronig and W. G. Penney, Proc. Roy. Soc. (London) A 130 (1931) 499; D. A McQuarrie, The Chemical Educator, vol. 1 (1996) S1430-4171.

[2] B. Kollmitzer and P. Hadley, Physica B, (2011)

[3] W. Magnus and S. Winkler, Hill's Equation, Dover 1966.