Reading
Kittel chapter 6: Free electron Fermi gas or R. Gross und A. Marx: Das freie Elektronengas
R. Gross und A. Marx: Sommerfeld Entwicklung
For the exam you should
- be familiar with the free electron model where the potential energy of the electrons is zero and the electron-electron interactions are ignored.
- be familiar with the solutions to the Schrödinger equation for the free electron model and know that the dispersion relation in this case is
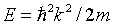 .
.
- be able to calculate the density of states for free electrons D(k) and D(E) in 1, 2, and 3 dimensions.
- be familiar with the fermi function.
- be able to start from the density of states and calculate the thermodynamic properties: chemical potential, internal energy, Helmholtz free energy, specific heat, entropy, pressure, and bulk modulus.
- know that the integrals that need to be solved to determine the thermodynamic properties cannot be solved analytically. They can be solved numerically or the Sommerfeld expansion can be used find approximations at low temperatures. You should know how to apply the Sommerfeld expansion.
- know that the form of the specific heat of a metal at low temperatures is cV = γT +AT³ and be able to explain the electron and phonon contribution. You should know how to calculate the effective mass from the specific heat.
- be familiar with ballistic and diffusive transport including the concepts of drift velocity, mobility, scattering time, mean free path, Matthiessen's rule, and umklapp scattering.
- be able to explain the Hall effect and how it can be used to measure the carrier concentration.
- be able to explain the thermal conductivity of metals, the Wiedemann-Franz law, and know what the Lorenz number is.
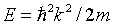 .
.