PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The Schrödinger equation can be solved for noninteracting particles confined to a line, a ring, a plane, a tube, or a three dimensional cube. Noninteracting particles confined to a line can be a useful approximation for electrons confined to a linear molecule. A ring can be used to describe electrons on a ring-like molecule such as benzene. Electrons trapped at an interface as they are in some transistors can be approximated by noninteracting particles confined to a plane. Electrons in a carbon nanotube can be described by electrons confined to a tube. Electrons in a quantum dot or electrons is a large piece of metal can be approximated by noninteracting particles confined to cube.
A particle of mass m confined to a line can be described by a one-dimensional infinite square well potential. The potential energy of the particle is infinite for x < 0 and x > L. For 0 < x < L, the potential energy of the particle is zero. The wavefunctions for a one-dimensional potential well are:
| ψn = √2/Lexp(-i2πEnt/h)sin | nπx | n = 1,2,3,... |
| L |
The energies that correspond to these wavefunctions can be determined by substituting the wavefunctions into the time-dependent Schrödinger equation. The energies are:
| En = | n²h² | = E1n² n = 1,2,3,... |
| 8mL² |
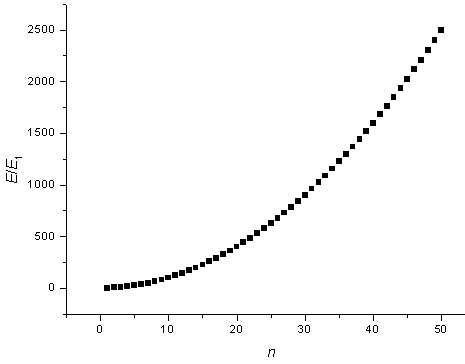
The energy states are plotted as a function of n.
The following form can be used to calculate the energies of a 1-d square well potential. For a potential well with the size of about one nanometer, the lowest energy levels are spaced at about 1 eV.
Density of states
Sometimes it is useful to know the number of states in a certain energy range. If the 1-d potential is very long (large L) then the states will be closely spaced and the number of states in a certain energy range can be approximated as a continuous function. By looking at the figure above it is clear that there are no states with energies below E1 = h²/(8mL²), there are many states just above E1 at the bottom of the parabola, and there are then fewer and fewer states as the energy increases.
This can be stated more mathematically by defining a function called the density of states g(E). The number of states between energies EA and EB is,
| EB | ||
| N = | ∫ | g(E)dE |
| EA |
Using the relationship for the energy, E = E1n², the density of states for a one-dimensional potential well can be determined to be,
| g(E) = | 1 | . |
| √EE1 |
Here a factor of 2 has been included to account for the two spins allowed for every value of n.
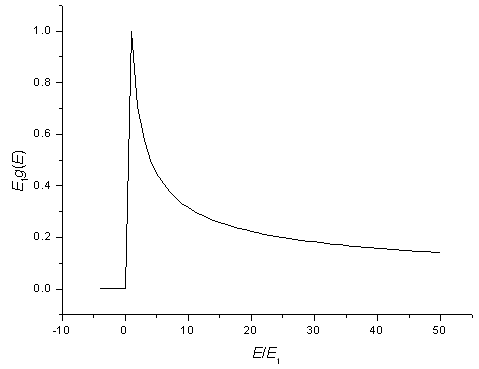
The density of states for a one-dimensional potential. The peak is called a Van Hove singularity.
The wavefunctions for a particle confined to a ring are,
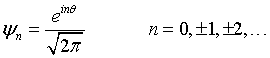
By substituting this into the Schrödinger equation,
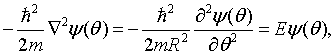
the energy eigenvalues can be determined to be,
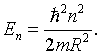
Here R is the radius of the ring. For n = 0 there are two degenerate energy eigenstates, one for each spin. For any other value of n there are four degenerate eigenstates, the two spin degenerate states for n and the two spin degenerate states for -n. Ring like molecules are therefore stable if they have 4n + 2 valence electrons. This is known in chemistry as Hückel's 4n + 2 rule. Molecules that satisfy this rule are called aromatic. Benzene is an example of an aromatic molecule.
For some one dimensional conductors like carbon nanotubes, it is appropriate to consider free electrons confined to a tube. The wavefunction must have a half integer number of wavelengths along the tube and an integer number of wavelengths around the tube. The wavefunctions describing this situation are,
| ψnφnx = | 1 | einφφ | sin | nxπx | nφ = ...-2,-1,0,1,2,... nx = 1,2,3,... |
| L |
This is one of the cases where it is essential that the wavefunction is complex. There are nodes in the wavefunction in the x-direction but there are no nodes in the wavefunction in the φ-direction. All of the eigenfunctions are symmetric in φ.
The energies can be found by substituting the wavefunction into the time independent Schrödinger equation. The energies are:
| Enxnφ = | h² | ( | nx² | + | nφ² | ) nx = 1,2,3,... nφ = ...-2,-1,0,1,2,... |
| 8m | L² | π²R² |
Here R is the radius of the tube.
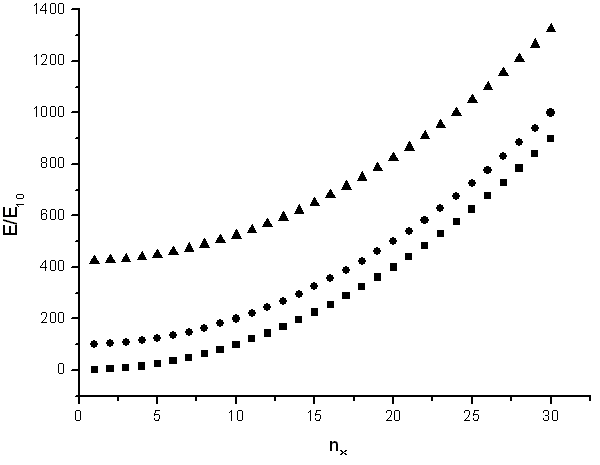
The energy states are ploted as a function of nx.
Density of states
Sometimes it is useful to know the number of states in a certain energy range. If the tube is very long (large L) then the states will be closely spaced and the number of states in a certain energy range can be approximated as a continuous function. By looking at the figure above it is clear that there are no states with energies below E11 = h²/(8m(L²+π²R²)), there are many states just above E11 at the bottom of the parabola, and there are then fewer and fewer states as the energy increases until the bottom of the next parabola is reached.
This can be stated more mathematically by defining a function called the density of states g(E). The number of states between energies EA and EB is,
| EB | ||
| N = | ∫ | g(E)dE |
| EA |
Using the relationship for the energy, Enk = E1kn², the density of states can be determined to be,
| g(E) = | Σ | Θ(E-E1k) | . |
| k | √EE1k |
Here Θ is the Heaviside step function and a factor of 2 has been included to account for the two spins allowed for every value of n.
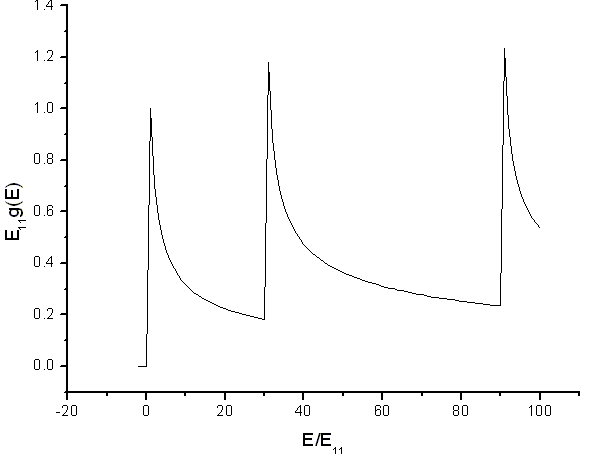
The density of states for electrons confined to a tube has shows peaks. The peaks are Van Hove singularities. The spacing of the peaks is related to the diameter of the tube.

Source: Electronic and transport properties of nanotubes, Jean-Christophe Charlier, Xavier Blase, and Stephan Roche, Rev. Mod. Phys. 79, p. 677 (2007).
For a particle of mass m confined to a square region of a plane, the potential energy is infinite for x < 0, y < 0, and x > Lx, or y > Ly. For 0 < x < Lx and 0 < y < Ly, the potential energy of the particle is zero. The wavefunctions for a two-dimensional infinite square well potential are:
| ψnxny = | 2 | exp(-i2πEnxnyt/h)sin | nxπx | sin | nyπy | nx,ny = 1,2,3,... |
| Lx | Ly |
The energies that correspond to these wavefunctions can be determined by substituting the wavefunctions into the time-dependent Schrödinger equation. The energies are:
| Enxny = | h² | ( | nx² | + | ny² | ) nx,ny = 1,2,3,... |
| 8m | Lx² | Ly² |
The energies can be caluated using the following form.
Density of states
The density of states for a two-dimensional potential square well is zero for energies below,
| E1 = | h² | ( | 1 | + | 1 | ) |
| 8m | Lx² | Ly² |
and is constant for energies above this energy. Including spin degeneracy the density of states is,
| g(E) = | 0 for E < E1 |
|
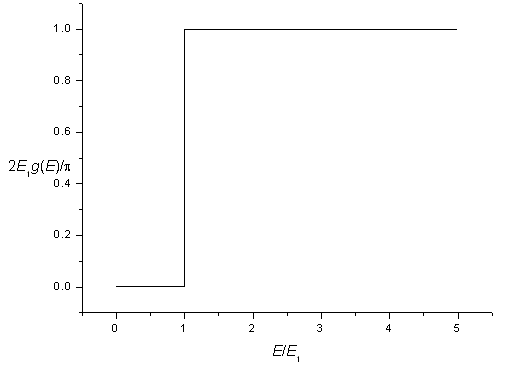
The density of states for a two-dimensional potential.
Paul Falstad's 2-D Rectangular Square Well Applet.
For a particle of mass m in an infinite 3-d square well potential, the potential energy of the particle is infinite for x < 0, y < 0, z < 0 and x > Lx, or y > Ly, z > Lz. For 0 < x < Lx,0 < y < Ly, and 0 < z < Lz, the potential energy of the particle is zero. The wavefunctions for a three-dimensional infinite square well potential are:3-d infinite square well
| ψnxnynz = | 2√2 | exp(-i2πEnxnynzt/h)sin | nxπx | sin | nyπy | sin | nzπz | nx,ny,nz = 1,2,3,... |
| Lx | Ly | Lz |
The energies that correspond to these wavefunctions can be determined by substituting the wavefunctions into the time-dependent Schrödinger equation. The energies are:
| Enxnynz = | h² | ( | nx² | + | ny² | + | nz² | ) nx,ny,nz = 1,2,3,... |
| 8m | Lx² | Ly² | Lz² |
The energies can be caluated using the following form.
Density of states
The density of states for a three-dimensional potential square well is zero for energies below,
| E1 = | h² | ( | 1 | + | 1 | + | 1 | ) |
| 8m | Lx² | Ly² | Lz² |
and increases as a square root above this energy. Including spin degeneracy the density of states is,
| g(E) = | 0 for E < E1 |
|
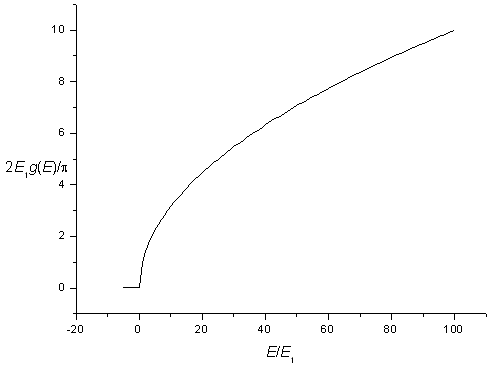
The density of states for a three-dimensional potential.