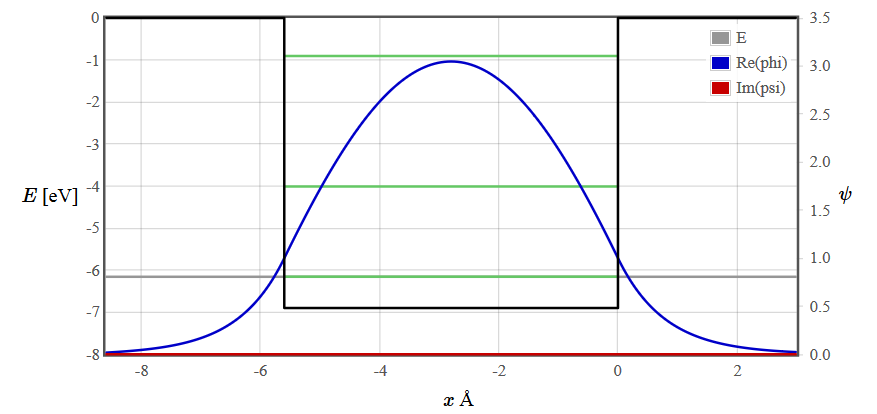
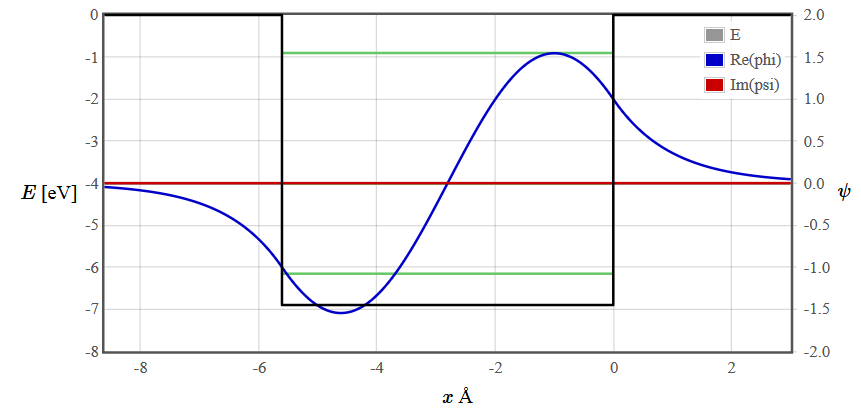
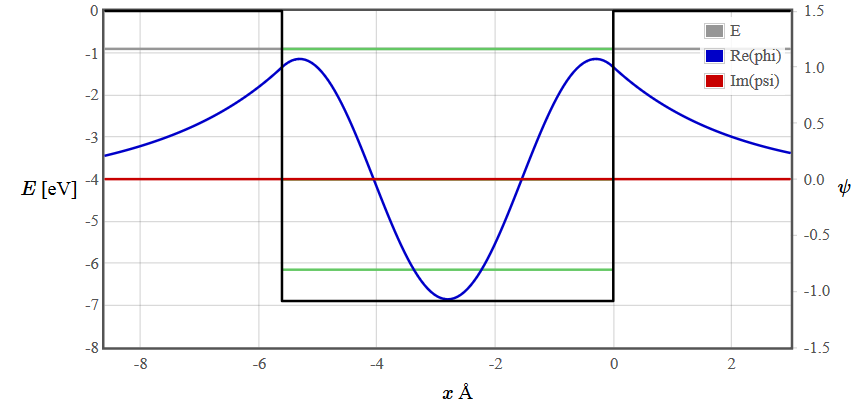
A finite rectangular potential well has a continuous spectrum of propagating solutions for $E > V_0$ but there are only a finite number of discrete bound states for $ E < V_0$. The energy levels of the bound states are drawn as green lines. The number of bound states depends on the width and depth of the well. There are solutions of the Schrödinger equation at every energy but for $E < V_0$ most are unphysical because the wave function diverges. To plot the wave function of a bound state, adjust the gray line representing the energy close to a green line using the slider or the course +++/--- buttons. Then continue adjusting the energy with the fine ++/-- and super fine +/- buttons until you find a symmetric or antisymmetric solution that does not diverge.

$E$ [eV]		$\psi$
	$x$ Å

$V_0=0$ [eV]			$L_0=4$ [Å]
$V_1=$ -5 [eV]			$L_1=$ 4 [Å]
$V_2=0$			$L_2=4$ [Å]

$E=$ -3 [eV]

10 Å^-1 10 Å^-1 10 Å^-1

The wave functions for the first three energy states are plotted below.