Many quantum particles in an infinite square well

One of the few analytically solvable problems in quantum mechanics is the infinite potential well, also known as a particle in a box. The Schrödinger equation is,

$$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} +V(x)\psi(x) = E\psi(x).$$

For the infinite potential well problem the potential $V(x)$ is defined to be zero in the interval $0 < x < L$ and infinite otherwise.

$$ V(x) = \begin{cases} 0 & 0 < x < L\\ \infty & \textrm{otherwise} \end{cases}$$

In one-dimension, the solutions are

$$\psi_n (x) = \begin{cases} \sqrt{\frac{2}{L}} \sin \left( \frac{n \pi x}{L} \right) & 0 < x < L \qquad n=1,2,3,\cdots\\ 0 & \text{otherwise} \end{cases} $$

Solutions can only be found at discrete energy levels. The energies can be found by subtituting the solutions into the Schrödinger equation,

$$ E_n = \frac{\hbar^2 \pi^2}{2mL^2} n^2.$$

As $n$ increases, the spacing between the energy levels increase because of the $n^2$ factor in the expression of the energy.

To describe one-dimensional solids, we consider the case where $L$ is very large and there are many electrons in the potential well. In this case, the energy levels become closely spaced and the number of electrons that could be placed in the potential well with an energy less than or equal to $E$ would be,

$$N(E) = \frac{2L}{\pi\hbar}\sqrt{2mE}.$$

There is a factor of 2 for spin but otherwise is this expression comes from solving the equation for $E_n$ for $n$.

It will be convenient to define an electron density of states $D(E)$ that tells us how many electron states there are between $E$ and $E+dE$ per unit length. If we add up all of the states up to an energy $E$, that should be $N(E)$.

$$N(E) = L\int\limits_0^E D(E')dE'$$

From this definition, $D(E)$ must be,

$$D(E) = \frac{1}{L}\frac{dN(E)}{dE} = \frac{1}{\hbar\pi}\sqrt{\frac{2m}{E}}.$$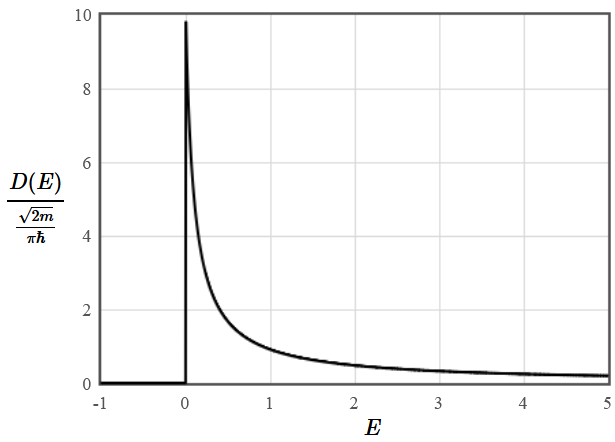

The density of states in one dimension falls like $\large \frac{1}{\sqrt{E}}$.

Two-dimensions

The infinite potential well problem can also be solved in 2- and 3-dimensions. The Schrödinger equation for the infinite square well in two dimensions contains two kinetic energy terms and no potential energy terms,

$$-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}-\frac{\hbar^2}{2m}\frac{d^2\psi}{dy^2} = E\psi.$$

This equation can be solved by the separation of variables and the solutions are products of the solutions for one-dimension.

$$\psi_{n_x n_y} (x,y) = \frac{2}{L} \:\sin \left(\frac{n_x \pi x}{L} \right) \: \sin \left(\frac{n_y \pi y}{L} \right)\qquad n_x,\,n_y = 1,2,3\cdots$$

The corresponding energy levels are, $$E_{n_x n_y} = \frac{\pi^2 \hbar^2}{2mL^2}\: \left(n_x^2 + n_y^2 \right).$$

If many electrons are in the lowest energy levels of a two-dimensional infinite square well, then the states will be filled to an energy $E$ which will correspond to a quarter circle in the $n_x - n_y$ plane.

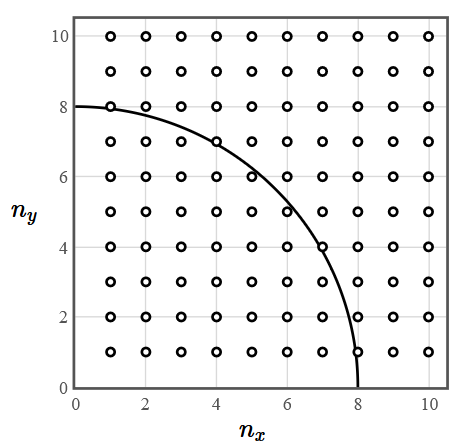
The radius of this circle is $n = \sqrt{\frac{2mL^2}{\pi^2\hbar^2}E}$ and the number of electron states inside the quarter circle is $2\frac{1}{4}\pi n^2$. There is a factor of 2 for spin. In terms of the energy, the number of electron states with an energy less than or equal to $E$ is,

$$N(E) = \frac{mL^2}{\pi\hbar^2}E.$$

In two dimensions the density of states is defined per unit area,

$$N(E) = L^2\int\limits_0^E D(E')dE'$$

From this definition, $D(E)$ must be,

$$D(E) = \frac{1}{L^2}\frac{dN(E)}{dE} = \frac{mL^2}{\pi\hbar^2}.$$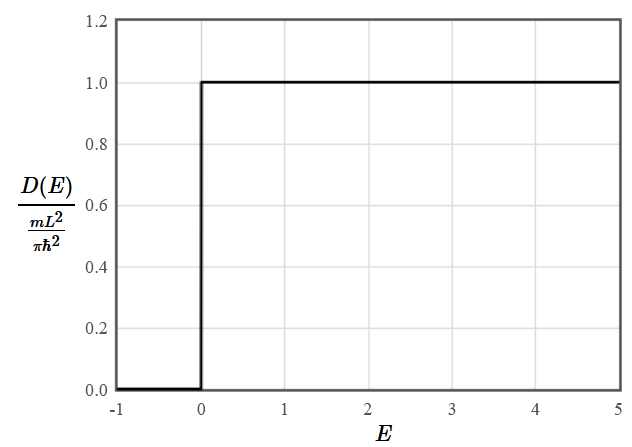

The density of states is constant in two dimensions.

Three-dimensions

In three dimensions the solutions are the product of three of the solutions to the one-dimensional problem,

$$\psi_{n_x n_y n_z} (x,y,z) = \sqrt{\frac{8}{L^3}} \:\sin \left(\frac{n_x \pi x}{L} \right) \: \sin \left(\frac{n_y \pi y}{L} \right) \: \sin \left(\frac{n_z \pi z}{L} \right)\qquad n_x,\,n_y,\,n_z = 1,2,3\cdots$$

When this solution is substituted into the Schrödinger equation, the energies can be calculated to be,

$$E_{n_x n_y n_z} = \frac{\pi^2 \hbar^2}{2mL^2}\: \left(n_x^2 + n_y^2 + n_z^2 \right).$$

The number of states with energy less than $E$ will correspond to the volume of one eighth of a sphere in $n_x -n_y -n_z$ space with a radius $n$ where,

$$n^2 = \frac{2mL^2}{\pi^2\hbar^2}E.$$

The number of electron states with an energy less than $E$ is,

$$N(E) = 2\frac{1}{8}\frac{4}{3}\pi n^3 = \frac{L^3}{3\pi^2\hbar^3}(2mE)^{\frac{3}{2}}.$$

There is a factor of 2 for spin. In three dimensions the density of states is defined per unit volume,

$$N(E) = L^3\int\limits_0^E D(E')dE'$$

From this definition, $D(E)$ must be,

$$D(E) = \frac{1}{L^3}\frac{dN}{dE} = \frac{(2m)^{\frac{3}{2}}}{2\hbar^3\pi^2}\sqrt{E}$$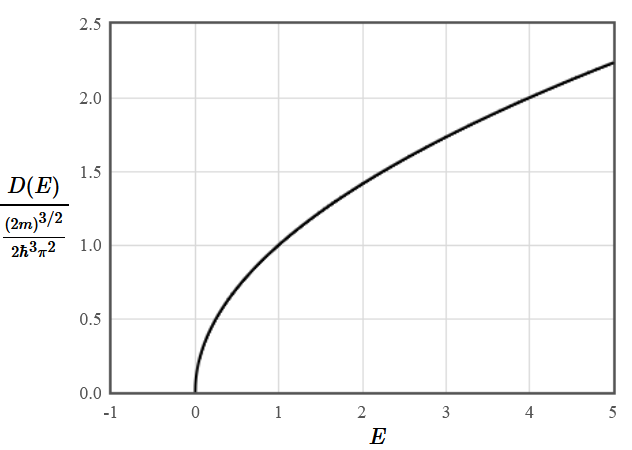

The density of states in three dimensions grows like $\sqrt{E}$.

A related problem is free particles in a box with periodic boundary conditions.

\(E\) [eV]		\( \psi\)
	\(x\) [Å]