Consider an electron moving in a periodic potential $V(x)$. The period of the potential is $a$, $V(x+a) = V(x)$. The Schrödinger equation for this case is,

\[ \begin{equation} -\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}+V(x)\psi =E\psi . \end{equation} \]

Quantum mechanically, the electron moves as a wave through the potential. Due to the diffraction of these waves, there are bands of energies where the electron is allowed to propagate through the potential and bands of energies where no propagating solutions are possible. The Bloch theorem states that the propagating states have the form,

\[ \begin{equation} \psi = e^{ikx}u_k(x). \end{equation} \]

where $k$ is the wavenumber and $u_k(x)$ is a periodic function with periodicity $a$.

The solutions to the Schrödinger equation for a 1-D periodic potential can be calculated numerically. The following form can be used to calculate the dispersion relation between $E$ and $k$ for any one dimensional potential. Input the periodic potential $V(x)$ in the interval between $0$ and $a$.

The density of states is,

\[ \begin{equation} D(E) = \frac{2}{\pi}\frac{dk}{dE}, \end{equation} \]

and the group velocity is,

\[ \begin{equation} v_g= \frac{1}{\hbar}\frac{dE}{dk}. \end{equation} \]

V(x) [eV] x [nm] The 1-D Potential Initial energy E1 =   [eV]  Final energy E2 =   [eV]  Mass m =   [kg]  Lattice constant a  =   [m]  Potential V(x)  =   [eV]  $E$ [eV] $ka$ $D(E)$ [eV-1 nm-1] The eigenvalues of the translation operator: $\lambda_+$    $\lambda_-$  $E$ $E$ $\alpha$    $\frac{2ma}{\hbar}v_g$  $E$ $E$ Data in 4 columns: $E$ [eV]  $ka$   $D(E)$ [1/(eV nm)]    $\frac{2mav_g}{\hbar}$

Standard mathematical functions abs(x), acos(x), asin(x), atan(x), cos(x), exp(x), log(x), pi = 3.141592653589793, pow(x,y) = x^y, round(x), sin(x), sqrt(x), tan(x) can be used in the form. In addition, the Heaviside step function H(x) can be used. Multiplication must be specified with a '*' symbol, 3*cos(x) not 3cos(x). Powers are specified with the 'pow' function: x² is pow(x,2) not x^2.

Some potentials that can be pasted into the form are given below.
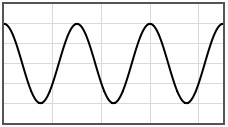
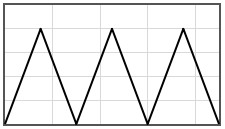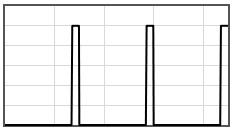
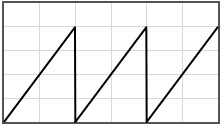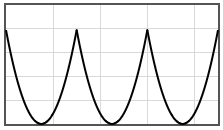
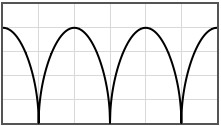