PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The quantization of the electromagnetic field is a central result in physics. It provides a unified picture of the wave nature and the particle nature of light. The derivation also serves as a template for the quantization of other fields. Many of the arguments presented here can be applied to phonons, magnons, plasmons, electrons, spinons, holons and other quantum particles that inhabit solids.
Review of electrodynamics
Electromagnetic fields are described by Maxwell's equations,
$$\nabla\cdot\vec{E}= \frac{\rho}{\epsilon_0}$$ $$\nabla\cdot\vec{B}= 0$$ $$\nabla\times\vec{E}= -\frac{\partial \vec{B}}{\partial t}$$ $$\nabla\times\vec{B}= \mu_0\vec{J}+\mu_0\epsilon_0\frac{\partial \vec{E}}{\partial t}$$The electric and magnetic fields can be expressed in terms of the vector potential $\vec{A}$ and the scalar potential $V$.
$$\vec{B}=\nabla\times\vec{A}$$ $$\vec{E}= -\nabla V-\frac{\partial\vec{A}}{\partial t}$$We consider electromagnetic waves in vacuum. The source terms then vanish and the electrostic potential is a constant that can be taken to be zero, $\rho=0$, $\vec{J}=0$, $V=0$. Expressed in terms of the vector potential, Maxwell's equations for this case are,
$$\nabla\cdot\frac{\partial\vec{A}}{\partial t}= 0$$ $$\nabla\cdot\nabla\times\vec{A}= 0$$ $$\nabla\times\frac{\partial\vec{A}}{\partial t}= \frac{\partial }{\partial t}\nabla\times\vec{A}$$ $$\nabla\times\nabla\times\vec{A}= -\mu_0\epsilon_0\frac{\partial^2\vec{A}}{\partial t^2}$$It is convenient to work in Coulomb gauge where $\nabla\cdot\vec{A}=0$. The first three of Maxwell's equations then reduce to identitites. Using the relation,
$$\nabla\times\nabla\times\vec{A} = \nabla(\nabla\cdot\vec{A})-\nabla^2\vec{A},$$the fourth equation takes the form of the wave equation,
\[ \begin{equation} c^2\nabla^2\vec{A}=\frac{\partial^2\vec{A}}{\partial t^2}. \end{equation} \]Here we have used the fact that $c^2=\frac{1}{\mu_0\epsilon_0}$. Solutions to the wave equation have the form,
\[ \begin{equation} \vec{A}\left(\vec{r},t\right)=\vec{A}\cos\left(\vec{k}\cdot\vec{r}-\omega t\right), \end{equation} \]where the relationship between $\omega$ and $\vec{k}$ is,
\[ \begin{equation} \omega = c|\vec{k}|. \end{equation} \]This relation between the frequency $\omega$ and the wavevector $\vec{k}$ is called the dispersion relation. It is linear for light waves propagating in vacuum. However, we have already seen that the dispersion equation for light, sound, electrons, neutrons, etc. is nonlinear when the waves propagate through a crystal because the waves diffract off the crystal.
The condition $\nabla\cdot\vec{A}=0$ requires the vector potential to be perpendicular to the propagation direction, $\vec{k}\cdot\vec{A}=0$.
For instance, for a wave propagating in the x-direction, the vector potential has the form,
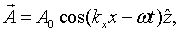
The electric and magnetic fields are both perpendicular to the propagation direction in this case,
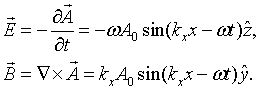

Quantization
To be able to quantize the electromagnetic field, it is convenient to expand the waves in normal modes. Consider a cubic metal cavity of length L on a side. Standing waves will exist in such a cavity. Electromagnetic waves do not penetrate into an ideal metal so only modes where the electric field is zero at the boundaries of the cavity are allowed. (The boundary conditions do not matter. The same results are found for a cavity with periodic boundary conditions.) The spatial part of the electric field has the form,
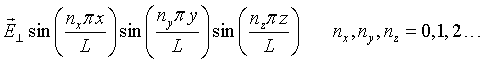
Consider a single mode specified by the mode numbers nx, ny, and nz and the polarization. For notational convenience, we will assign a unique integer s to each mode. Substituting this mode into the wave equation results in the following equation,
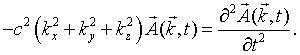
Here kx = nxπ/L, ky = nyπ/L, and kz = nzπ/L. The choice of the polarization plus the fact that the vector potential must be perpendicular to the propagation vector k restricts the vector potential to point in a specific direction. This above equation is mathematically equivalent to the equation for a one-dimensional harmonic oscillator. If A is replaced by x,
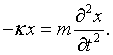
If two classical equations of motion can be put into correspondence this way then the quantum equations of motion are related by the same correspondence and it is possible to simply transcribe the familiar harmonic oscillator solutions to the case of electromagnetic waves. The allowed quantum energy levels for a one-dimensional harmonic oscillator are

where
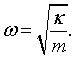
Transcribing this back to the problem of a single mode of the electromagnetic field we find that the allowed quantum energies for the mode are also,

but in this case the frequency is,
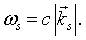
The integer j represents the number of photons in mode s. Since photons are bosons, the mean number of photons in a particular mode is given by the Bose-Einstein factor,
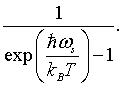
The total energy is the energy E = hω/2π = hc/λ of a mode, times the probability that the mode is occupied, summed over all possible modes.
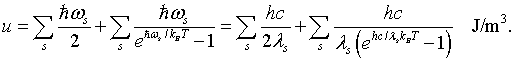
The first sum is the zero point energies of the harmonic oscillators. In order to evaluate the sum, it is convenient to convert it to an integral. To do this the number of modes at every frequency or every wavelength will be calculated.
Density of states
We can determine how many modes there are at every frequency if we know how many modes there are for every wavenumber k. When periodic boundary conditions are applied to a cube of length L, an integer number of wavelengths must fit in the cube, λ = L/n, where n is an integer. This restricts the allowed wavevectors to kx, ky, kz = 2πn/L. These allowed values of k form a cubic lattice in k space. The k space volume associated with each point is (2π/L)³.
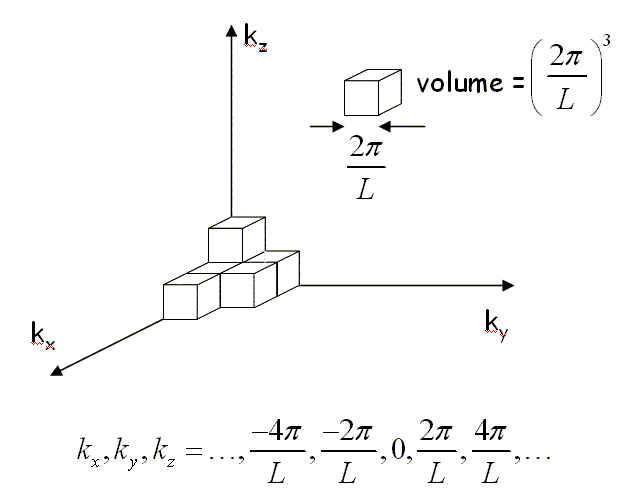
There are twice as many linearly independent normal modes as there are points in k-space because the electric field has two independent components that are perpendicular to the propagation direction. The number of allowed modes with k values between k and k + dk is,
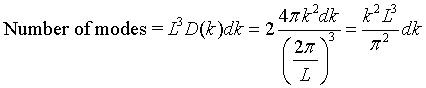
Here D(k) is called the density of states. The density of states can also be expressed in terms of frequency. The number of states per unit volume with a a frequency between ω and ω + dω is,
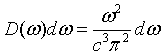
Expressed in terms of wavelength, the number of states per unit volume with a a wavelength between λ and λ + dλ is,
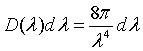
Planck's radiation law
The energy density between λ and λ + dλ is the energy E=hc/λ of a mode times the density of states, times the probability that the mode is occupied.
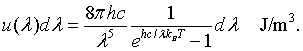
This is Planck's famous formula for the energy density of a blackbody.
|
This plot was generated for an object with a temperture of 5700 K. That is the temperture of the surface of the sun. The peak in the spectrum is then in the visible at about 0.5 μm (green). The form above can be used to generate Planck curves for other temperatures. Put 310 K = 37 C into the form to see the spectrum of radiation you are emitting right now. The wavelength at the peak of the distribution can be found by differentiating the expression for the energy density and setting the result equal to zero. The result is known as Wien's law.
λmaxT = 0.0028977 m K
This is used, for instance, to determine the temperature of distant stars.
The intensity radiated by a blackbody has the same wavelength dependence as the energy density. The intensity radiated between λ and λ + dλ is c/4 times the energy density,
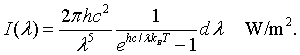
By integrating the intensity over all wavelengths it is possible to determine the total intensity of electromagnetic waves radiated by a blackbody at a specific temperaure.
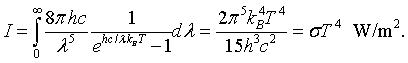
This is known as the Stefan-Boltzmann law. The Stefan-Boltzmann constant is σ = 5.67 × 10-8 J/(m2 K4). Similarly the toal energy density is,
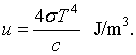
Thermodynamic properties
Once the distribution of microscopic quantum levels are known, it is possible to calculate many thermodynamic quantities. In general, this is done by constructing a partition function that takes the appropriate average over all of the microscopic states. Partition functions are beyond the scope of this course so we will simply state that the Helmholtz free energy is,
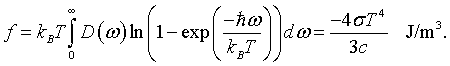
The derivation of this result is found in books on statistical mechanics. The entropy is related to the Helmholtz free energy by,
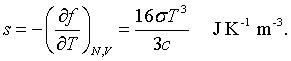
It is possible to construct the internal energy from either the free energy and the entropy, u = f +Ts, or by summing over all states.
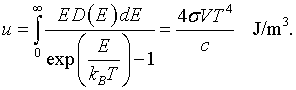
Each photon has a momentum,
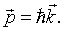
When the photons strike the walls of the cavity they therefore exert a pressure. The radiation pressure is,
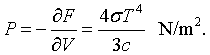
Finally, a certain amount of energy must be added to the cavity to increase the temperature. This is described by the specific heat.
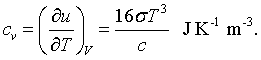
Recipe for the quantization of fields
The above derivation includes many important results but it also serves as a recipe for quantizing fields. The steps in this recipe are:
The results for the quantization of the wave equation in 1-, 2-, and 3-dimensions are summarized in the following table.
1-D | 2-D | 3-D | |
Wave Equation | $\large c^2\frac{\partial^2 A_j}{\partial x^2}=\frac{\partial^2 A_j}{\partial t^2}$ | $\large c^2\left(\frac{\partial^2 A_j}{\partial x^2}+\frac{\partial^2 A_j}{\partial y^2}\right)=\frac{\partial^2 A_j}{\partial t^2}$ | $\large c^2\left(\frac{\partial^2 A_j}{\partial x^2}+\frac{\partial^2 A_j}{\partial y^2}+\frac{\partial^2 A_j}{\partial z^2}\right)=\frac{\partial^2 A_j}{\partial t^2}$ |
Eigenfunction solutions | $\large A_j=\exp (i(kx-\omega t))$ | $\large A_j=\exp (i(\vec{k}\cdot\vec{r}-\omega t))$ | $\large A_j=\exp (i(\vec{k}\cdot\vec{r}-\omega t))$ |
Dispersion relation | $\large \omega=ck$ | $\large \omega=c|\vec{k}|$ | $\large \omega=c|\vec{k}|$ |
Density of states | $\large D(k)=\frac{2}{\pi}$ | $\large D(k)=\frac{k}{\pi}$ [m-1] | $\large D(k)=\frac{k^2}{\pi^2}$ [m-2] |
Density of states |
|
|
|
Density of states |
|
|
|
Density of states |
|
|
|
Chemical potential | μ = 0 | μ = 0 | μ = 0 |
Internal energy distribution |
|
|
|
Internal energy |
|
|
|
Intensity spectral density |
|
|
|
Wien's law |
|
|
|
Stefan - Boltzmann law |
|
| $\large I=\frac{2\pi^5k_B^4T^4}{15c^2h^3}=\sigma T^4\text{ [J m}^{-2}\text{s}^{-1}\text{]}$ |
Specific heat |
|
|
|
Helmholtz free energy |
|
|
|
Entropy |
|
|
|
Pressure |
|
|
|
The equations for 1-, 2-, and 3-dimensions have been programmed below. Modify the temperature and wavelength as necessary and press the 'execute' button to perform the calculation.
|
| ||
Script Output | ||