The eigenfunction solutions of the Schrödinger equation for free electrons are plane waves,

\[ \begin{equation} \psi(\vec{r}) = e^{i\vec{k}\cdot\vec{r}}. \end{equation} \]

If the $\vec{k}$ vector is outside the first Brillouin zone, the plane wave solution can be written in Bloch form with a vector $\vec{k}'$ inside the first Brillouin zone,

\[ \begin{equation} \psi(\vec{r}) = e^{i\vec{k}'\cdot\vec{r}}e^{i\vec{G}\cdot\vec{r}}, \end{equation} \]

where $\vec{k}=\vec{k}'+\vec{G}$. By writing every plane wave as a Bloch wave with a $\vec{k}$ vector inside the First Brillouin zone, the dispersion relation can be expressed as,

\[ \begin{equation} E =\frac{\hbar^2(\vec{k}'+\vec{G})^2}{2m}, \end{equation} \]

where every reciprocal lattice vector $\vec{G}$ produces a different band in the first Brillouin zone.

The resulting dispersion relations for some Bravais lattices are shown below. A parabola of the form $E+\hbar^2|\vec{k}-\vec{G}|/2m$ is drawn at every reciprocal lattice point $\vec{G}$. Cuts are made through this family of parabolas in the high symmetry directions to plot the dispersion relation in those directions. Click on the buttons to choose a different order for the symmetry points.

1-D	2-D square
2-D hexagonal	General 2D lattice
Simple cubic	Face centered cubic
Body centered cubic	Hexagonal
Tetragonal	Body Centered Tetragonal
Orthorhombic	Simple Monoclinic

Some examples of the utility of the empty lattice approximation are shown below.

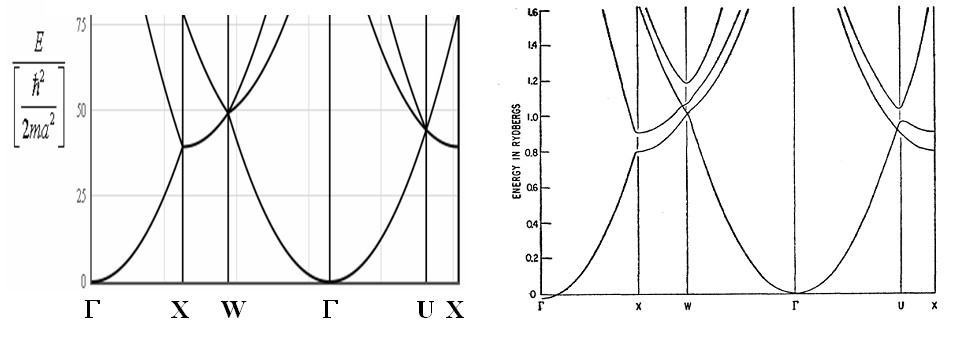
On the left is the empty lattice approximation for an fcc crystal and on the right is the calculated band structure of aluminum (an fcc metal). The right image was taken from W.A. Harrison, Physical Review, vol. 118 pp. 1182-1189 (1960).