Singlet and triplet states
The first excited state of helium has one electron in a 1s orbital and one electron in a 2s orbital. There are four possible spin configurations for this state: $\uparrow\uparrow$, $\downarrow\downarrow$, $\downarrow\uparrow$, and $\uparrow\downarrow$. The corresponding wavefunctions are,

\[ \begin{equation} \begin{matrix} \Psi_{\uparrow\uparrow}=\frac{1}{\sqrt{2}}\left|\begin{matrix} \phi_{1s}^{\text{He}}\uparrow(\vec{r}_1) & \phi_{2s}^{\text{He}}\uparrow(\vec{r}_1) \\ \phi_{1s}^{\text{He}}\uparrow(\vec{r}_2) & \phi_{2s}^{\text{He}}\uparrow(\vec{r}_2) \end{matrix}\right| = \frac{1}{\sqrt{2}}(\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)-\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2))\uparrow\uparrow, \\ \\ \Psi_{\downarrow\downarrow}=\frac{1}{\sqrt{2}}\left|\begin{matrix} \phi_{1s}^{\text{He}}\downarrow(\vec{r}_1) & \phi_{2s}^{\text{He}}\downarrow(\vec{r}_1) \\ \phi_{1s}^{\text{He}}\downarrow(\vec{r}_2) & \phi_{2s}^{\text{He}}\downarrow(\vec{r}_2) \end{matrix}\right| = \frac{1}{\sqrt{2}}(\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)-\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2))\downarrow\downarrow, \\ \\ \Psi_{\uparrow\downarrow}=\frac{1}{\sqrt{2}}\left|\begin{matrix} \phi_{1s}^{\text{He}}\uparrow(\vec{r}_1) & \phi_{2s}^{\text{He}}\downarrow(\vec{r}_1) \\ \phi_{1s}^{\text{He}}\uparrow(\vec{r}_2) & \phi_{2s}^{\text{He}}\downarrow(\vec{r}_2) \end{matrix}\right| = \frac{1}{\sqrt{2}}(\phi_{1s}^{\text{He}}(\vec{r}_1)\uparrow\phi_{2s}^{\text{He}}(\vec{r}_2)\downarrow-\phi_{2s}^{\text{He}}(\vec{r}_1)\downarrow\phi_{1s}^{\text{He}}(\vec{r}_2)\uparrow), \\ \\ \Psi_{\downarrow\uparrow}=\frac{1}{\sqrt{2}}\left|\begin{matrix} \phi_{1s}^{\text{He}}\downarrow(\vec{r}_1) & \phi_{2s}^{\text{He}}\uparrow(\vec{r}_1) \\ \phi_{1s}^{\text{He}}\downarrow(\vec{r}_2) & \phi_{2s}^{\text{He}}\uparrow(\vec{r}_2) \end{matrix}\right| = \frac{1}{\sqrt{2}}(\phi_{1s}^{\text{He}}(\vec{r}_1)\downarrow\phi_{2s}^{\text{He}}(\vec{r}_2)\uparrow-\phi_{2s}^{\text{He}}(\vec{r}_1)\uparrow\phi_{1s}^{\text{He}}(\vec{r}_2)\downarrow). \end{matrix} \end{equation} \]

The first two wavefunctions, $\Psi_{\uparrow\uparrow}$ and $\Psi_{\downarrow\downarrow}$, have an antisymmetric orbital component and a symmetric spin component. It is not possible to directly separate the last two wavefunctions, $\Psi_{\uparrow\downarrow}$ and $\Psi_{\downarrow\uparrow}$, into a product of an orbital component and a spin component but they can be transformed to a wavefunction with an antisymmetric orbital component and a symmetric spin component,

\[ \begin{equation} \Psi_{\uparrow\downarrow+\downarrow\uparrow}= \frac{1}{2}(\Psi_{\uparrow\downarrow}+\Psi_{\downarrow\uparrow})=\frac{1}{\sqrt{2}}((\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)-\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2))(\uparrow\downarrow+\downarrow\uparrow), \end{equation} \]

and a wavefunction with a symmetric orbital component and an antisymmetric spin component,

\[ \begin{equation} \Psi_{\uparrow\downarrow-\downarrow\uparrow}= \frac{1}{2}(\Psi_{\uparrow\downarrow}-\Psi_{\downarrow\uparrow})=\frac{1}{\sqrt{2}}((\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)+\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2))(\uparrow\downarrow-\downarrow\uparrow). \end{equation} \]

The wavefunctions $\Psi_{\uparrow\uparrow}$, $\Psi_{\downarrow\downarrow}$, $\Psi_{\uparrow\downarrow+\downarrow\uparrow}$, and $\Psi_{\uparrow\downarrow-\downarrow\uparrow}$ span the same space of functions that the wavefunctions $\Psi_{\uparrow\uparrow}$, $\Psi_{\downarrow\downarrow}$, $\Psi_{\uparrow\downarrow}$, and $\Psi_{\downarrow\uparrow}$ do so either set can be used to describe the first excited state of helium. We will work with the set of wavefunctions: $\Psi_{\uparrow\uparrow}$, $\Psi_{\downarrow\downarrow}$, $\Psi_{\uparrow\downarrow+\downarrow\uparrow}$, and $\Psi_{\uparrow\downarrow-\downarrow\uparrow}$.

The orbital components of wavefunctions $\Psi_{\uparrow\uparrow}$, $\Psi_{\downarrow\downarrow}$, and $\Psi_{\uparrow\downarrow+\downarrow\uparrow}$ are antisymmetric and are all identical, only their spin components are different. Spin does not appear in the total Hamiltonian so the energies of these three states must be the same. These three form the triplet state. The energy of wavefunction $\Psi_{\uparrow\downarrow-\downarrow\uparrow}$, the singlet, evaluates to be higher than the other three. This is because the antisymmetric orbital wavefunction is zero when $\vec{r}_1=\vec{r}_2$ so the electron-electron repulsion is smaller for the antisymmetric orbital wavefunction.

$a_0^{3}\Psi_{\text{He}}$
	$\frac{r}{a_0}$

Plots of the single and triplet wavefunction assuming that the 2s electron sees an effective nuclear charge of $Z_{\text{eff}}=1.15.$

Three energy diagrams for helium. On the left are the energies of the atomic orbitals evaluated with $H_{\text{red}}^{\text{He}}$. In the center are the energies of the atomic orbitals evaluated with $H_{\text{total}}^{\text{He}}$. On the right are the true eigen energies for helium.

Exchange energy
Consider the energy difference between the singlet state and the triplet state.

\[ \begin{equation} \Delta E = \langle \Psi_{\uparrow\downarrow-\downarrow\uparrow}|H_{\text{total}}^{\text{He}}|\Psi_{\uparrow\downarrow-\downarrow\uparrow}\rangle - \langle \Psi_{\uparrow\uparrow}|H_{\text{total}}^{\text{He}}|\Psi_{\uparrow\uparrow}\rangle \end{equation} \]

Substituting in the symmetric orbital component for $\Psi_{\uparrow\downarrow-\downarrow\uparrow}$ and the antisymmetric orbital component for $\Psi_{\uparrow\uparrow}$ yields,

\[ \begin{equation} \Delta E = \frac{1}{2}\langle \phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)+\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2)|H_{\text{total}}^{\text{He}}|\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)+\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2) \rangle \\ - \frac{1}{2}\langle \phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)-\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2)|H_{\text{total}}^{\text{He}}|\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)-\phi_{2s}^{\text{He}}(\vec{r}_1)\phi_{1s}^{\text{He}}(\vec{r}_2) \rangle. \end{equation} \]

After some algebra, this reduces to,

\[ \begin{equation} \Delta E = \langle \phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2)|H_{\text{total}}^{\text{He}}|\phi_{1s}^{\text{He}}(\vec{r}_2)\phi_{2s}^{\text{He}}(\vec{r}_1) \rangle +\langle \phi_{1s}^{\text{He}}(\vec{r}_2)\phi_{2s}^{\text{He}}(\vec{r}_1)|H_{\text{total}}^{\text{He}}|\phi_{1s}^{\text{He}}(\vec{r}_1)\phi_{2s}^{\text{He}}(\vec{r}_2) \rangle. \end{equation} \]

The difference in energy only depends on matrix elements where the electrons at $\vec{r}_1$ and $\vec{r}_2$ get exchanged in the $\langle$bra| and the |ket$\rangle$. For this reason, $\Delta E$ is referred to as twice the exchange energy.

More accurate calculations
To determine the states of helium more accurately, we can look for better atomic orbitals. The atomic orbitals that we have used so far neglect the electron-electron interactions. The electrons will partially screen the positive nucleus so the true wavefunction will have a larger diameter than the one that was calculated neglecting the electron-electron interactions. This suggests that we use an atomic orbital of the form,

\[ \begin{equation} \sqrt{\frac{Z_e^3}{\pi a_0^3}}\exp\left(-\frac{Z_er}{a_0}\right), \end{equation} \]

where $Z_e$ is the effective charge of the nucleus. The energy of the helium ground state is minimized for $Z_e=1.69$. There are a number of numerical techniques like the Hartree Fock method or density functional theory that can be used to find better atomic orbitals. It is known, however, that the true ground state of any interacting electron system cannot be written in terms of products of atomic orbitals because it will include factors like $(\vec{r}_1-\vec{r}_2)^2$ which cannot be written as a product of two functions like $\phi_m(\vec{r}_1)\phi_n(\vec{r}_2)$. Calculating the true wavefunctions that are not written as atomic orbitals is a very computationally intensive process.

When a magnetic field is applied, a term must be added to the Hamiltonian that couples to the spin. The ground state has zero magnetic moment so its energy does not change in a magnetic field. The triplet state splits into three energy levels due to the Zeeman effect. There are also some small details in atomic spectra like the spin-orbit interaction and the hyperfine interaction that will not be discussed further here.

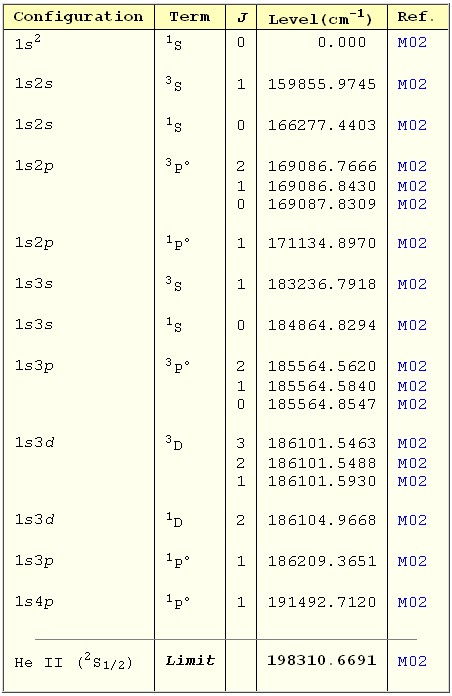
The energy levels for He from physics.nist.gov

Next: Review of atomic physics (Many-electron atoms)

---

A description of the hydrogen atom and many-electron atoms can be found in The Physics of Atoms and Quanta by H. Haken and H. C. Wolf.