The valence electrons moving in a crystal experience a periodic potential. The Schrödinger equation for an electron moving in a one-dimensional potential is,

$$-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}+V(x)\psi =E\psi ,$$

where the potential is periodic $V(x+a) = V(x)$ with periodicity $a$.

Mathematically, this falls into the same category of differential equations as the problem of a child on a swing (Second order linear differential equations with periodic coefficients). It is useful first to consider the more familiar problem of the swing, which, for small amplitudes, is described by the linear differential equation,

$$m\frac{d^2\theta}{dt^2}+b \frac{d\theta}{dt}+\frac{mg}{l}\theta =0.$$

Here $m$ is the mass of the child, $b$ is a damping constant, $g$ is the acceleration of gravity at the earth's surface, and $l$ is the length of the rope that is holding the swing. If an adult gives the child a single push, and the child sits passively on the swing, the amplitude of the oscillations will decay exponentially.

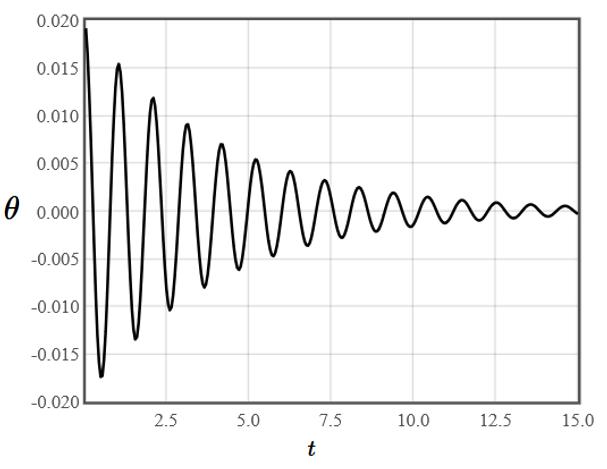
To keep the swing going, the child can pump the swing. This involves pulling back on the ropes periodically to raise the mass of the child. Alternatively, you can describe pumping the swing as a periodic modulation of the length of the rope $l(1-A\cos(\Omega t))$. Here $a$ is the amplitude of the modulation of the length of the rope and $\Omega$ is the angular frequency of the modulation. The differential equation becomes,

$$m\frac{d^2\theta}{dt^2}+b \frac{d\theta}{dt}+\frac{mg}{l(1-A\cos(\Omega t))}\theta =0.$$

If the driving frequency $\Omega$ is too fast or too slow, the amplitude of the oscillations remains small. However, if $\Omega$ is a multiple of the resonant frequency of the swing, large amplitude oscillations will occur. The driving frequency does not have to be exactly the resonant frequency of the swing. There is a range of frequencies $\Omega$ that will cause large amplitude oscillations.

Large amplitude oscillations are induced when the modulation is about twice the resonance frequency. For most parameters, no parametric amplification is observed.

$m=$ 1 [kg]
$b=$ 0.2 [kg/s]
$l=$ 0.5 [N/m]
$A=$ 0.4 [N]
$\Omega=$ 7.5 [rad/s]

The resonance frequency is $\omega=\sqrt{g/l-b^2/4m^2}=$ 4.43 rad/s.

Press the to increase $\Omega$ and notice that the oscillations remain small until $\Omega$ is about twice the resonance frequency $\omega$. There is a finite range of $\Omega$ for which large amplitude oscillations are generated. Returning to the problem of electrons in a periodic potential, there are ranges of energies where the amplitude of the electron wave function remains bounded, and there are other ranges of energies where the electron wave function increases exponentially. The ranges where the amplitude remains bounded are called bands, and the ranges where the amplitude grows exponentially are called band gaps. If periodic boundary conditions are applied to a crystal, the exponentially growing solutions are unphysical. If a finite crystal with surfaces is considered, the exponentially growing solutions describe the exponential decay of the electron probability from the surfaces. Electrons with energies in the band gap are not found in the interior of the crystal.