PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The thermodynamic properties depend dramatically on the number of electrons per primitive unit cell $n$. For the same dispersion relation and density of states, the crystal can be a metal, a semiconductor, or an insulator depending on the number of electrons per primitive unit cell.
This is illustrated for an electron confined to a potential of the form,
$$V(f_{\text{square}}(x) + f_{\text{square}}(y) + f_{\text{square}}(z)),$$where $V = V_2 - V_1$ is the amplitude of the potential and $f_{\text{square}}(x)$ is a square wave function.
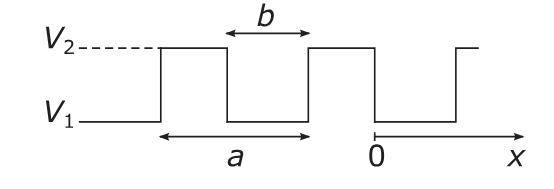
This potential has the advantage that the density of states can be easily calculated for a given set of parameters $V$ and $b/a$. [1]
Increase the amplitude of the potential with the button until band gaps appear. Then change the number of electrons with the and buttons and notice that the thermodynamic properties change dramatically if the chemical potential falls in the band gap.
|
| |
|
| |
|
|