The diffraction condition,

$$\vec{k}'-\vec{k} = \vec{G},$$

can be drawn as an isosceles triangle,

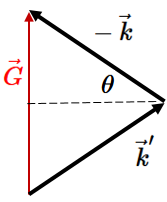
where the angle between $\vec{k}$ and $\vec{k}'$ is $2\theta$. A little trigonometry shows,

$$\frac{|\vec{G}_{hkl}|}{2} = |\vec{k}|\sin\theta.$$

Since $d_{hkl} = \frac{2\pi}{|\vec{G}_{hkl}|}$ and $\lambda = \frac{2\pi}{|\vec{k}|}$, this can also be written as,

$$\lambda = 2d_{hkl}\sin\theta.$$

This equation has a nice interpretation in terms of reflections from the lattice planes.

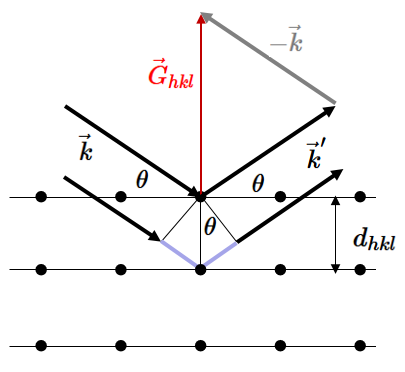
X-rays travelling in the direction $\vec{k}$ strike lattice planes at an angle $\theta$ to the horizontal. The x-rays reflect off the lattice planes. For these reflections, the angle of incidence equals the angle of reflection. If we consider rays that reflect off two adjacent lattice planes as shown in the diagram above, the lower ray travels a longer distance $2d_{hkl}\sin\theta$ compared to the upper ray. The extra distance is drawn in blue in the diagram. These two rays will add constructively at the detector if this extra distance is equal to an integer number of wavelengths,

$$n\lambda = 2d_{hkl}\sin\theta .$$

This is the condition for Bragg diffraction and is almost the same formula as was presented above. In the Bragg formula, $d_{hkl}$ is restricted to lattice planes, so the indices $h$, $k$, and $l$ must have no common divisor. When the indices have no common divisor, they are called Miller indices. When the indices can have a common divisor, they are called Laue indices, and the diffraction condition takes the form $\lambda = 2d_{hkl}\sin\theta$. Laue indices can be constructed from the Miller indices by multiplying by an integer $n = 1,2,3\cdots$.