A reciprocal lattice vector $\vec{G}$ points in a direction in space indicating which way the waves are moving. There are an infinite number of planes that can be defined perpendicular to $\vec{G}$. For every positive or negative real number $C$, there is a plane consisting of points $\vec{r}_C$ which satisfies the condition,

$$\vec{G}\cdot\vec{r}_C = C.$$

This can be written as $|\vec{G}||\vec{r}_C|\cos\theta$ where $\theta$ is the angle between $|\vec{G}|$ and $|\vec{r}_C|$. If $|\vec{G}|$ is held constant, this can be interpreted graphically as saying that $|\vec{r}_C|\cos\theta$, the component of $\vec{r}_C$ in the direction of $\vec{G}$, is also constant.

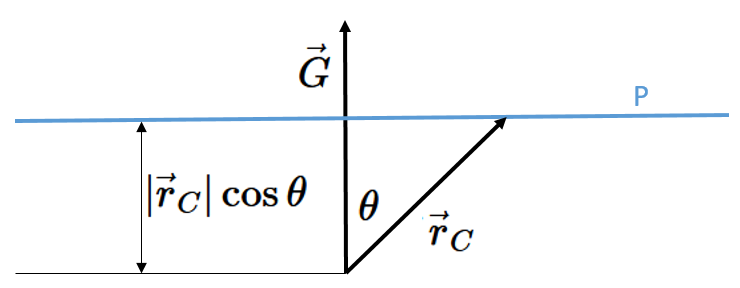
There are special planes called netplanes where,

$$\vec{G}\cdot\vec{r}_n = 2\pi n,\qquad n=\cdots\, -2,\,-1,\,0,\,1,\,2,\,\cdots.$$

These are special planes because the Bravais lattice points always fall on a netplane. The Bravais lattice point at,

$$\vec{T} = u\vec{a}_1 + v\vec{a}_2 + w\vec{a}_3$$

Lies in the plane

$$\vec{G}\cdot\vec{T} = \left( h\vec{b}_1 + k\vec{b}_2 + l\vec{b}_3\right)\cdot \left(u\vec{a}_1 + v\vec{a}_2 + w\vec{a}_3\right)= 2\pi(hu+kv+wl).$$

Since $(hu+kv+wl)$ is always an integer, the Bravais lattice points lie on a netplane.

The distance between netplanes $d_{hkl}$ can be calculated by considering $n=1$ and $\theta = 0$, then,

$$|\vec{G}_{hkl}||\vec{r}|\cos\theta= |\vec{G}_{hkl}|d_{hkl}= 2\pi,$$

and the distance bewteen the netplanes is,

$$d_{hkl}= \frac{2\pi}{|\vec{G}_{hkl}|}.$$

Below are some Bravais lattice points with a few netplanes drawn in.

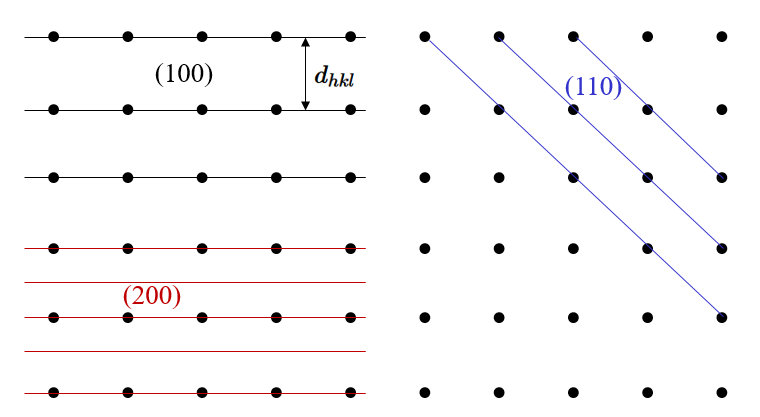
Notice that the Bravais lattice points always fall on the netplanes, but in some cases (like 200), there are planes with no Bravais lattice points on them. The netplanes that contain Bravais lattice points are called lattice planes. A set of netplanes will be lattice planes if $h$, $k$, and $l$ are coprime. A three-dimensional crystal can be thought of as being a stack of lattice planes.

The lattice planes remind us of the planes that are defined by Miller indices, and in fact, they are the same. Consider a plane that cuts the $\vec{a}_1$ axis at point $p_1$, the $\vec{a}_2$ axis at point $p_2$, and the $\vec{a}_3$ axis at point $p_3$. These three points define a plane perpendicular to a $\vec{G}$ vector defined by $\vec{G}\cdot\vec{r}_C = C$. Substituting the three points where the plane cuts the axes, we have,

$$\vec{G}\cdot p_1\vec{a}_1 = C = 2\pi h p_1,\\ \vec{G}\cdot p_2\vec{a}_2 = C = 2\pi k p_2,\\ \vec{G}\cdot p_3\vec{a}_3 = C = 2\pi l p_3.$$

This can be solved for $h$, $k$, and $l$.

$$h = \frac{C}{2\pi p_1},\\ k = \frac{C}{2\pi p_2},\\ l = \frac{C}{2\pi p_3}.$$

The integers $h$, $k$, and $l$ are the coprime integers that have the same ratio as $1/p_1$, $1/p_2$, $1/p_3$. This was the definition of the Miller integers.

This means that $\vec{G}_{hkl}$ is normal to the $(hkl)$ plane. Bravais lattice points in the $(hkl)$ plane will be perpendicular to $\vec{G}_{hkl}$,

$$ \vec{G}_{hkl}\cdot\vec{T}_{uvw} = 0 =\left( h\vec{b}_1 + k\vec{b}_2 + l\vec{b}_3\right)\cdot \left(u\vec{a}_1 + v\vec{a}_2 + w\vec{a}_3\right)= 2\pi(hu+kv+wl),$$

so the lattice vector $\vec{T}_{uvw}$ is in the $(hkl)$ plane if $(hu+kv+wl)=0$. This is known as the Weiss zone law.