PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
For powder diffraction, a sample that may contain several crystals is ground into a fine powder so that there are many small crystals with random orientations. X-rays strike the surface of the powder at an angle θ, and an x-ray detector is placed at an angle θ to the surface.
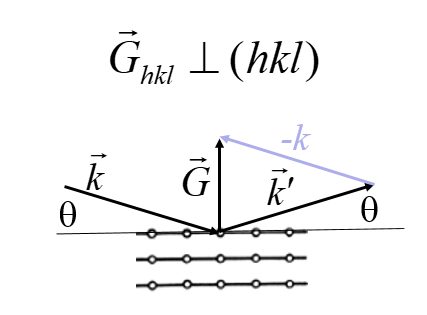
Only lattice planes parallel to the surface will diffract x-rays to the detector. By changing the angle θ, there will be a peak in the measured x-ray intensity every time the distance $d_{hkl}$ satisfies $\lambda = 2d_{hkl}\sin\theta$. This does not provide enough information to determine the crystal structure of the crystals in the sample. However, if the crystal structure has already been determined, the powder diffraction pattern provides a fingerprint that can be used to identify the presence of a crystal. In a typical application, a sample of unknown composition is ground into a fine powder and some analysis software compares the measured powder diffraction pattern to a database. The software tries to match the measurement to a superposition of powder diffraction patterns found in the database.
Powder diffraction patterns can be found, for instance, at the American Mineralogist Crystal Structure Database. A typical entry in the database is shown below.
Aluminum
Wyckoff R W G
Crystal Structures 1 (1963) 7-83
Second edition. Interscience Publishers, New York, New York
Cubic closest packed, ccp, structure
_database_code_amcsd 0011136
CELL PARAMETERS: 4.0496 4.0496 4.0496 90.000 90.000 90.000
SPACE GROUP: Fm3m
X-RAY WAVELENGTH: 1.541838
Cell Volume: 66.409
Density (g/cm3): 2.698
MAX. ABS. INTENSITY / VOLUME**2: 34.61439413
RIR: 4.177
RIR based on corundum from Acta Crystallographica A38 (1982) 733-739
2-THETA INTENSITY D-SPACING H K L Multiplicity
38.50 100.00 2.3380 1 1 1 8
44.76 47.49 2.0248 2 0 0 6
65.16 28.01 1.4317 2 2 0 12
78.30 30.71 1.2210 3 1 1 24
82.52 8.74 1.1690 2 2 2 8
================================================================================
XPOW Copyright 1993 Bob Downs, Ranjini Swaminathan and Kurt Bartelmehs
For reference, see Downs et al. (1993) American Mineralogist 78, 1104-1107.
The Multiplicity column indicates how many diffraction peaks have the same value of $d_{hkl}$. For instance, the first diffraction peak in the file is is listed as $hkl = (111)$ but all eight planes $(111),\,(11-1),\,(1-11),\,(1-1-1),\,(-111),\,(-11-1),\,(-1-11),\,(-1-1-1)$ have same value of $d_{hkl}$ and can't be distinguished in a powder diffraction measurement.
Below is a form that can be used to calculate the powder diffraction pattern of a crystal with up to five atoms in the basis.
Primitive reciprocal lattice vectors
| $\vec{b}_1=2\pi\frac{\vec{a}_2\times\vec{a}_3}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1] |
| $\vec{b}_2=2\pi\frac{\vec{a}_3\times\vec{a}_1}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1] |
| $\vec{b}_3=2\pi\frac{\vec{a}_1\times\vec{a}_2}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1] |
The script first calculates the primitive reciprocal lattice vectors from the primitive lattice vectors in real space. Then for each reciprocal lattice vector $\vec{G} = h\vec{b}_1+k\vec{b}_2+l\vec{b}_3$, the structure factor $n_{\vec{G}}$ is calculated. All reciprocal lattice vectors with the same absolute value diffract x-rays at the same angle. In the table below, $N$ is the number of reciprocal lattice vectors that have contribute to the diffraction signal for a certain angle θ. $d_{hkl} = 2\pi/|\vec{G}_{hkl}|$ is the distance between the $hkl$ netplanes.
Structure factors
$G_{hkl}$ Å-1 |
$d_{hkl}$ Å |
$2\theta$ |
$|n_{\vec{G}}|$ |
$I=N|n_{\vec{G}}|^2$ |
Multiplicity |