There are fourteen Bravais lattices in three dimensions. A three-dimensional periodic function can be described with a Fourier series of the form,

$$f(\vec{r})=\sum \limits_{\vec{G}} f_{\vec{G}}\exp \left(i\vec{G}\cdot\vec{r}\right),$$

where the Fourier coefficients are given by,

$$f_{\vec{G}} = \frac{1}{V_{\text{uc}}}\int\limits_{\text{unit cell}}f(\vec{r})\exp (-i\vec{G}\cdot \vec{r})d\vec{r}.$$

Example 1: Cubes repeated on a bcc lattice

Cubes are arranged on a bcc lattice such that the corners of the cubes just touch. This is a three-dimensional analog to the square wave problem that was solved in one dimension.

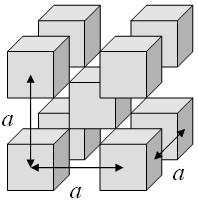
A three-dimensional periodic function $f(\vec{r})$ is defined such that it has a constant value $C$ inside the cubes and is zero outside the cubes. This function can be expressed as a Fourier series,

$$f(\vec{r})=\sum \limits_{\vec{G}} f_{\vec{G}}\exp \left(i\vec{G}\cdot\vec{r}\right),$$

The Fourier coefficients f_G are given by,

$$f_{\vec{G}}=\frac{1}{V}\int f_{\text{unit cell}}(\vec{r})\exp\left(-i\vec{G}\cdot\vec{r}\right)d^3r = \frac{2C}{a^3}\int\limits_{-\frac{a}{4}}^{\frac{a}{4}}\int\limits_{-\frac{a}{4}}^{\frac{a}{4}}\int\limits_{-\frac{a}{4}}^{\frac{a}{4}}\exp\left(-iG_xx\right)\exp\left(-iG_yy\right)\exp\left(-iG_zz\right)dxdydz.$$

The cube at the origin lies entirely within the Wigner-Seitz cell, and the function $f(\vec{r})$ is zero outside the cube, so we just need to integrate over the cube. The integrals over $x$, $y$, and $z$ are easily performed.

$$f_{\vec{G}}=\frac{16C\sin\left(\frac{G_xa}{4}\right)\sin\left(\frac{G_ya}{4}\right)\sin\left(\frac{G_za}{4}\right)}{a^3G_xG_yG_z}.$$

This result can readily be generalized to any rectangular cuboid with dimensions $L_x\times L_y\times L_z$ that is repeated on any three-dimensional Bravais lattice. As long as a primitive unit cell can be defined such that the cuboid is entirely within the cell, the Fourier series for a function that has the value $C$ inside the cuboids and zero outside the cuboids is,

$$f(\vec{r})=\sum\limits_{\vec{G}}\frac{8C\sin\left(\frac{G_xL_x}{2}\right)\sin\left(\frac{G_yL_y}{2}\right)\sin\left(\frac{G_zL_z}{2}\right)}{VG_xG_yG_z}\exp\left(i\vec{G}\cdot\vec{r}\right).$$

Here $V$ is the volume of the primitive unit cell.

 

Example 2: spheres on an fcc lattice

Spheres of radius $R$ are arranged on a fcc lattice.

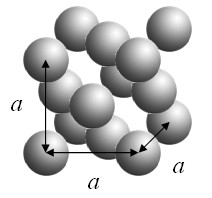
A three-dimensional periodic function $f$ is defined such that it has a constant value $C$ inside the spheres and is zero outside the spheres. This function can be expressed as a Fourier series,

$$f(\vec{r})=\sum \limits_{\vec{G}} f_{\vec{G}}\exp \left(i\vec{G}\cdot\vec{r}\right).$$

The Fourier coefficients $f_{\vec{G}}$ are given by,

$$f_{\vec{G}}=\frac{1}{V}\int f_{\text{unit cell}}(\vec{r})\exp\left(-i\vec{G}\cdot\vec{r}\right)d^3r = \frac{C}{V}\int\limits_{\text{sphere}}\exp\left(-i\vec{G}\cdot\vec{r}\right)d^3r.$$

As long as the spheres do not overlap, a primitive unit cell can be defined so that the sphere at the origin lies entirely within the primitive unit cell. Since the function $f$ is zero outside the sphere, we just need to integrate over the sphere.

$$f_{\vec{G}}= \frac{C}{V}\int\limits_{0}^R\int\limits_{0}^{\pi}\int\limits_{-\pi}^{\pi}\exp\left(-i\vec{G}\cdot\vec{r}\right)r^2\sin \theta drd\theta d\phi.$$

The integral over $\phi$ is easily performed.

$$f_{\vec{G}}= \frac{2\pi C}{V}\int\limits_{0}^R\int\limits_{0}^{\pi}\left(\cos\left(|G|r\cos\theta\right) -i\sin\left(|G|r\cos\theta\right)\right)r^2\sin \theta drd\theta.$$

Recognizing that,

$$\dfrac{d}{d\theta}\cos\left( |G|r\cos\theta\right)=|G|r\sin\left(|G|r\cos\theta\right)\sin\theta\qquad\text{and}\\ \dfrac{d}{d\theta}\sin\left( |G|r\cos\theta\right)=-|G|r\cos\left(|G|r\cos\theta\right)\sin\theta,$$

the integral over $\theta$ can be performed.

$$f_{\vec{G}}= \frac{4\pi C}{V}\int\limits_{0}^R\frac{\sin\left(|G|r\right)}{|G|r}r^2dr.$$

Finally, performing the integral over $r$,

$$f_{\vec{G}}= \frac{4\pi C}{V}\frac{\sin\left(|G|r\right)-|G|R\cos\left(|G|r\right)}{|G|^3}.$$

As long as the spheres do not overlap, the Fourier series for spheres repeated on any Bravais lattice is,

$$f(\vec{r})=\frac{4\pi C}{V}\sum \limits_{\vec{G}}\frac{\sin\left(|G|r\right)-|G|R\cos\left(|G|r\right)}{|G|^3}\exp\left(i\vec{G}\cdot\vec{r}\right).$$

 

Example 3: Cylinders repeated on a Bravais lattice

Consider cylinders that don't overlap, repeated on a Bravais lattice. The cylinders have a length $L$, a radius $R$, and the axis of the cylinders lies along the $z$-axis. A function $f$ is defined to be a constant $C$ inside the cylinders and zero outside the cylinders. The Fourier coefficients for this periodic pattern are,

$$f_{\vec{G}} = \frac{1}{V_{\text{uc}}} \int f_{cell}(\vec{r})\exp\left(-i\vec{G}\cdot\vec{r}\right)d^3r.$$

Use cylindrical coordinates $\rho= \sqrt{x^2+y^2}$, $\theta = \mathrm{atan}(y/z)$, $z$ where the axis of the cylinder is along the $z$-axis.

$$f_{\vec{G}} = \frac{C}{V_{\text{uc}}}\int_{0}^{2\pi}\int_{0}^R\int_{-L/2}^{L/2}\exp(-iG_zz)\left(\cos(G_{\rho}\rho\cos(\theta)) + i\sin(G_{\rho}\rho\cos(\theta))\right)\rho\,d\theta d\rho dz$$

Here $G_{\rho} = \sqrt{G_x^2+G_y^2}$. Integrating over $z$ yields,

$$f_{\vec{G}} = \frac{2C}{V_{\text{uc}}}\frac{\sin\left(\frac{G_zL}{2}\right)}{G_z}\int_{0}^{2\pi}\int_{0}^R\left(\cos(G_{\rho}\rho\cos(\theta)) + i\sin(G_{\rho}\rho\cos(\theta))\right)\rho\,d\theta d\rho.$$

Integrating over $\theta$ yields,

$$f_{\vec{G}} = \frac{4\pi C}{V_{\text{uc}}}\frac{\sin\left(\frac{G_zL}{2}\right)}{G_z }\int_{0}^R\rho J_0(G_{\rho}\rho) d\rho.$$

Here $J_0(x)$ is the zeroth order Bessel function of the first kind. Integrating over $\rho$ yields ,

$$f_{\vec{G}} = \frac{4\pi C}{V_{\text{uc}}}\frac{\sin\left(\frac{G_zL}{2}\right)}{G_z}\frac{RJ_1(G_{\rho}R)}{G_{\rho}},$$

where $J_1(x)$ is the first-order Bessel function of the first kind. It is convenient to rewrite this in terms of the $\mathrm{sinc}(x)= \frac{\sin(\pi x)}{\pi x}$ function and the $\mathrm{jinc}(x) = \frac{J_1(x)}{x}$ function.

$$f_{\vec{G}} = \frac{2\pi CR^2L}{V_{\text{uc}}}\mathrm{sinc}\left(\frac{G_zL}{2\pi}\right)\mathrm{jinc}(G_{\rho}R).$$

 

Example 4: Total electron density

The total electron density in a crystal is a periodic function. Most of the electrons in a solid are core electrons that are very tightly bound to the nuclei. To a good approximation, the total electron density of an atom can be described by a Gaussian function $\frac{Z}{r_0^3 \pi^{3/2}}\exp (-r^2/r_0^2)$, where $Z$ is the number of electrons of the atom. The integral of this function over all space is $Z$. Typically, the width $r_0$ of the Gaussian is so much smaller than the lattice constant $a$ that the integral of this function over a unit cell is also about $Z$. The electron density of the basis of a crystal is,

$$n_{u.c.}(\vec{r})=\frac{1}{V_{\text{u.c.}}}\sum \limits_j \frac{Z_j}{r_{0j}^3 \pi^{3/2}}\exp \left(-\frac{(\vec{r}-\vec{r}_j)^2}{r_{0j}^2}\right),$$

where $j$ sums over the atoms in the basis and $\vec{r}_j$ is the position of atom $j$. The constant $\frac{Z_j}{r_{0j}^3 \pi^{3/2}}$ in front of the Gaussian is chosen so that when the electron density is integrated over the unit cell, the Gaussians around each atom contribute an amount $Z_j$ to the integral. The sum is then $\sum\limits_j Z_j$. Dividing this sum by the volume of the unit cell, $V_{u.c.}$, the electron density is obtained.

The Fourier coefficients can be found by multiplying both sides of this equation by $\exp (-i\vec{G}\cdot\vec{r})$ and integrating over a unit cell. The result is,

\[ \begin{equation} n_{\vec{G}}=\frac{1}{V_{\text{u.c.}}^2}\sum \limits_j Z_j\exp \left(-\frac{r_{0j}^2G^2}{4}\right)\exp (-i\vec{G}\cdot\vec{r}_j). \end{equation} \]

The square of the Fourier coefficients $|n_{\vec{G}}|^2$ is proportional to the intensity of a diffraction peak in an x-ray diffraction experiment. Since the volume of the unit cell is the same for all of the Fourier coefficients and only their ratio is important for x-ray diffraction, it is usual to leave the factor of $1/V_{\text{u.c.}}^2$ out and define the structure factor $S_{\vec{G}}$ as,

\[ \begin{equation} S_{\vec{G}}= V_{\text{u.c.}}^2n_{\vec{G}}=\sum \limits_j Z_j\exp \left(-\frac{r_{0j}^2G^2}{4}\right)\exp (-i\vec{G}\cdot\vec{r}_j). \end{equation} \]

The structure factor for $\vec{G}=0$ is the number of electrons per unit cell,

\[ \begin{equation} S_{\vec{G}=0}=\sum \limits_j Z_j. \end{equation} \]

Since the Gaussians are sharply peaked around the nuclei, sometimes the electron density is approximated by a collection of $\delta$-functions,

\[ \begin{equation} n_{u.c.}(\vec{r})=\frac{1}{V_{\text{u.c.}}}\sum \limits_j Z_j\delta(\vec{r}-\vec{r}_j). \end{equation} \]

In this case, the structure factors are,

\[ \begin{equation} S_{\vec{G}}=\sum \limits_j Z_j\exp (-i\vec{G}\cdot\vec{r}_j). \end{equation} \]

 

Example 5: The molecular orbital Hamiltonian

An important periodic function is the periodic potential that appears in the molecular orbital Hamiltonian for a crystal. For a crystal containing only one atom in the basis, the potential is,

\[ \begin{equation} U(\vec{r})=-\frac{Ze^2}{4\pi \epsilon_0}\sum \limits_j\frac{1}{|\vec{r}-\vec{r}_j|}. \end{equation} \]

Here $\vec{r}_j$ are the positions of the atoms. The periodic potential is formed by the Coulomb potentials of the nuclei, each with a positive charge of $Ze$. The Fourier series for this potential is,

\[ \begin{equation} U(\vec{r})=-\frac{Ze^2}{V_{u.c.} \epsilon_0}\sum \limits_{\vec{G}}\frac{\exp (i\vec{G}\cdot\vec{r})}{|\vec{G}|^2}. \end{equation} \]

 

Example 6: Muffin tin potentials

A muffin tin is used to bake muffins.

 

Wikimedia

In solid-state physics, a 2-D muffin tin potential is a potential consisting of a lattice of circular regions. Within the circular regions, the potential is a Coulomb potential with the form -Ze²/(4πεr) and between the circular regions, the potential is constant. The constant is chosen so that there is no discontinuity in the potential. This potential looks like a muffin tin.

In three dimensions, a muffin tin potential U(r) is a lattice of spherical regions where the potential inside the spheres is -Ze²/(4πεr) and outside the spheres the potential is constant.

The integral that must be performed to determine the Fourier coefficients is,

$$U_{\vec{G}}=\frac{4\pi}{V}\int\limits_0^R\frac{-Ze^2}{4\pi\epsilon_0r}\frac{\sin\left(|G|r\right)}{|G|r}r^2dr+\frac{4\pi}{V}\int\limits_0^R\frac{-Ze^2}{4\pi\epsilon_0R}\frac{\sin\left(|G|r\right)}{|G|r}r^2dr$$

The first term is the radial Fourier transform of the Coulomb potential, and the second term adds a constant value to the potential in the spherical regions to match the Coulomb potential to the zero potential outside the spherical regions.

The Fourier series for a muffin tin potential is,

$$U(\vec{r})=\frac{Ze^2}{V\epsilon_0} \sum\limits_{\vec{G}}\left(\frac{\cos(|G|R)-1}{|G|^2}+\frac{\sin(|G|R)-|G|R\cos(|G|R)}{R|G|^3}\right)\exp\left(i\vec{G}\cdot\vec{r}\right).$$

 

Example 7: Woodpile

A woodpile consists of rectangular rods in the $x$-direction and rectangular rods in the $y$-direction stacked on top of each other.

The woodpile can be constructed by repeating the unit cell,

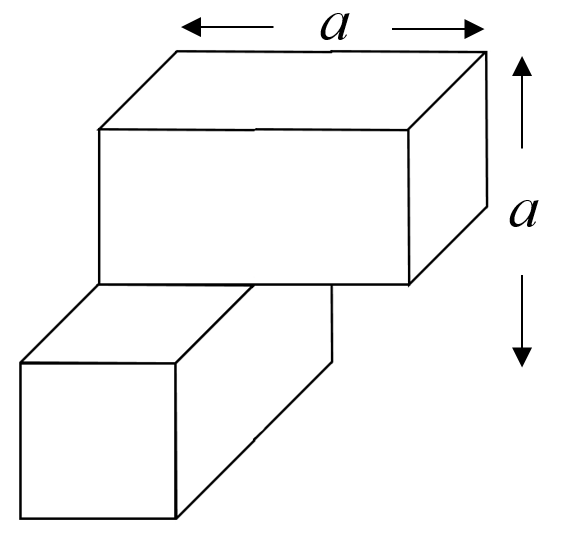
on a body-centered tetragonal Bravais lattice where the conventional unit cell has the dimensions $a\times a \times 2a$. The primitive lattice vectors and the primitive reciprocal space lattice vectors can be defined to be,

$$\vec{a}_1 = \frac{a}{2}(\hat{x}+\hat{y})-a\hat{z},\qquad \vec{a}_2 = \frac{a}{2}(\hat{x}-\hat{y})+a\hat{z},\qquad \vec{a}_3 = \frac{a}{2}(-\hat{x}+\hat{y})+a\hat{z},$$ $$ \vec{b}_1 = \frac{2\pi}{a}(\hat{k_x}+\hat{k_y}),\qquad \vec{b}_2 =\frac{2\pi}{a}\hat{k_x}+\frac{\pi}{a}\hat{k_z},\qquad \vec{b}_3 = \frac{2\pi}{a}\hat{k_y}+\frac{\pi}{a}\hat{k_z}.$$

The reciprocal lattice vectors are labeled by three integers $\vec{G}_{n_1n_2n_3} = n_1\vec{b}_1 + n_2\vec{b}_2 + n_3\vec{b}_3$. The $x$-, $y$-, and $z$-components of $\vec{G}_{n_1n_2n_3}$ are,

$$ G_x = \frac{2\pi}{a}(n_1 +n_2), \qquad G_y =\frac{2\pi}{a}(n_1 +n_3),\qquad G_z =\frac{\pi}{a}(n_2 +n_3).$$

The unit cell consists of one rectangular solid in the $x$-direction with dimensions $L_x =a$, $L_y =a/2$, $L_z =a/2$ and one rectangular solid in the $y$-direction with dimensions $L_x =a/2$, $L_y =a$, $L_z =a/2$. The Fourier series for a rectangular solid on any Bravais lattice was calculated above to be,

$$f(\vec{r}) = \sum_{\vec{G}}\frac{8C\sin\left(\frac{G_xLx}{2}\right)\sin\left(\frac{G_yLy}{2}\right)\sin\left(\frac{G_zLz}{2}\right)}{VG_xG_yG_z}e^{i\vec{G}\cdot\vec{r}}.$$

It was assumed that the function $f$ has a value $C$ inside the rectangular solid and zero outside. The rectangular solid was centered on the Bravais lattice point. Here $V$ is the volume of the primitive unit cell. For a single rod lying in the $x$-direction, the Fourier coefficients are,

$$f_{n_1,n_2,n_3} = \frac{C}{4}\mathrm{sinc}\left(n_1 +n_2\right)\mathrm{sinc}\left((n_1 +n_3)/2\right)\mathrm{sinc}\left((n_2 +n_3)/4\right).$$

Here $\mathrm{sinc}(x)= \frac{\sin(\pi x)}{\pi x}$ is called a sinc function and has the interesting property that it is zero for all integer values $x$ except for $x = 0$ where it is 1.

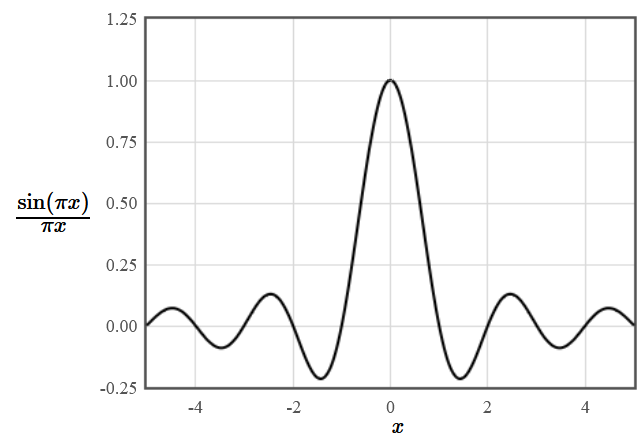
There is a similar calculation for the rods in the $y$-direction. For a single rod centered at the Bravais lattice point, the structure factors are,

$$f_{n_1,n_2,n_3} = \frac{C}{4}\mathrm{sinc}\left((n_1 +n_2)/2\right)\mathrm{sinc}\left((n_1 +n_3)\right)\mathrm{sinc}\left((n_2 +n_3)/4\right).$$

If the rod in the $x$-direction is centered on a Bravais lattice point, then the rod in the $y$-direction has to be shifted by $\vec{r}_0 = \frac{a}{2}\hat{x} - \frac{a}{2}\hat{y} + \frac{a}{2}\hat{z}$ to form the unit cell. If the center of the rod is shifted by $\vec{r}_0$, the structure factor is multiplied by a factor $e^{-i\vec{G}\cdot\vec{r}_0}$.

The structure factors of the rod in the $y$-direction have to be multiplied by,

$$e^{-i\pi(\frac{3}{2}n_2-\frac{1}{2}n_3)}.$$

The rod in the $x$-direction does not overlap with the rod in the $y$-direction, so the Fourier series of the woodpile is the sum of the two Fourier series,

$$f_{n_1,n_2,n_3} = \frac{C}{4}\mathrm{sinc}\left(n_1 +n_2\right)\mathrm{sinc}\left((n_1 +n_3)/2\right)\mathrm{sinc}\left((n_2 +n_3)/4\right)\\ +\frac{C}{4}\mathrm{sinc}\left((n_1 +n_2)/2\right)\mathrm{sinc}\left((n_1 +n_3)\right)\mathrm{sinc}\left((n_2 +n_3)/4\right)e^{-i\pi(\frac{3}{2}n_2-\frac{1}{2}n_3)}.$$

The nonzero structure factors are tabulated below for $C=$.

$n_1$ $n_2$ $n_3$    $f_{\vec{G}}$      $f_{\vec{G}}^2$