Electrons

Electrons are often thought of as little particles, but a more precise statement of the nature of electrons is that they move like waves and exchange energy and momentum like particles. When an electron is confined by a potential $V(x)$, it is described by a wavefunction. The wavefunction is a solution to the Schrödinger equation,

$$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} +V(x)\psi(x) = E\psi(x).$$

Here $m$ is the mass of the electron, $E$ is the energy of the electron, and $\psi$ is the wavefunction. The probability of finding the electron at position $x$ is $\psi^*\psi$.

One of the few analytically solvable problems in quantum mechanics is the infinite potential well, also known as a particle in a box. For this problem, the potential $V(x)$ is defined to be zero in the interval $0 < x < L$ and infinite otherwise.

$$ V(x) = \begin{cases} 0 & 0 < x < L\\ \infty & \textrm{otherwise} \end{cases}$$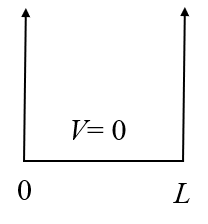

In one dimension, the solutions are

$$\psi_n (x) = \begin{cases} \sqrt{\frac{2}{L}} \sin \left( \frac{n \pi x}{L} \right) & 0 < x < L \qquad n=1,2,3,\cdots\\ 0 & \text{otherwise} \end{cases} $$

Solutions can only be found at discrete energy levels. The energies can be found by substituting the solutions into the Schrödinger equation,

$$ E_n = \frac{\hbar^2 \pi^2}{2mL^2} n^2.$$

As $n$ increases, the spacing between the energy levels increases because of the $n^2$ factor in the expression of the energy.

As more electrons are added to the well, they fill the energy levels following the Pauli exclusion principle. Two electrons first occupy the lowest energy level, then two electrons in the next lowest energy level, etc.

\(E\) [eV]		\( \psi\)
	\(x\) [Å]