So far in this chapter on lattice vibrations, we have examined two one-dimensional cases, but real crystals are three-dimensional. We need to find the normal modes of three-dimensional crystals. To specify the $x-$, $y-$, and $z-$coordinates of the $N$ atoms in a crystal requires $3N$ normal modes. In each of these normal modes, all of the atoms in the crystal oscillate with the same frequency. From our experience with the one-dimensional cases, we expect that the normal modes will have a wave-like character. Consider a simple cubic crystal with one atom in the basis, a lattice constant of $a$, and the dimensions $L\times L\times L$. If we apply periodic boundary conditions to the normal modes, then there can be one wavelength in a distance $L$, two wavelengths in a distance $L$, etc. The wavevectors that correspond to the wave-like solutions that satisfy the periodic boundary conditions are,

$$k_x,\,k_y,\,k_z=-\frac{\pi}{a}\cdots -\frac{6\pi}{L}, -\frac{4\pi}{L}, -\frac{2\pi}{L}, 0, \frac{2\pi}{L}, \frac{4\pi}{L}, \frac{6\pi}{L},\cdots\frac{\pi}{a}$$

There is a shortest wavelength allowed in this problem corresponding to neighboring atoms oscillating 180° out of phase with each other. Atoms in this mode are arranged up-down-up-down: 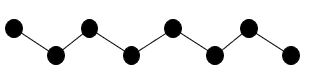The wavelength of this mode is $2a$ (from an up atom to an up atom) and the corresponding wavevector is $k=\frac{\pi}{a}$. Since the reciprocal lattice point closest to the origin is at $G=\frac{2\pi}{a}$, $k=\frac{\pi}{a}$ is on the Brillouin zone boundary, and all of the allowed $\vec{k}$-vectors that satisfy the periodic boundary conditions are in the first Brillouin zone. Although the discussion has been limited to a simple cubic crystal, it is generally true that the allowed wavevectors for the phonon normal modes are only those wavevectors in the first Brillouin zone. For the simple cubic case, the number of wavenumbers that satisfy the periodic boundary conditions in the first Brillouin zone is the volume of the Brillouin zone $\left(\frac{2\pi}{a}\right)^3$ divided by the volume associated with one allowed $\vec{k}$ vector, $\left(\frac{2\pi}{L}\right)^3$. The number of allowed $\vec{k}$ vectors in the first Brillouin zone is $\left(\frac{2\pi}{a}\right)^3\left(\frac{L}{2\pi}\right)^3 =N$, the number of primitive unit cells in the crystal. While this was calculated for simple cubic for simplicity, it is also generally true that the number of allowed $\vec{k}$ vectors (that satisfy the periodic boundary conditions) in the first Brillouin zone is the number of primitive unit cells in the crystal.

Each of the $N$ allowed $\vec{k}$ vectors can have three polarizations. There is one longitudinal polarization where the atoms can oscillate in the direction of $\vec{k}$, and there are two transverse polarizations, where the atoms oscillate in the two directions perpendicular to $\vec{k}$. For every $\vec{k}$, there is one longitudinal and two transverse modes. These are the $3N$ phonon normal modes we need to be able to describe the arbitrary motion of the $N$ atoms in the crystal.

The normal modes should be eigenfunctions of the translation operator. This leads us to postulate normal modes of the form,

$$\vec{u}_{lmn} = \vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right).$$

Here $\vec{u}_{lmn}$ is the displacement of atom $lmn$ from its equilibrium position and $\vec{k}$ is a wavevector in the first Brillouin zone that satisfies the periodic boundary conditions. We can check that this is an eigenfunction of the translation operator by translating the normal mode by a translation vector $\vec{T}_{pqr} = p\vec{a}_1 + q\vec{a}_2 + r\vec{a}_3$,

$$\mathbf{T}_{pqr}\vec{u}_{lmn} =\vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot(p+1)\vec{a}_1+m\vec{k}\cdot(q+1)\vec{a}_2+n\vec{k}\cdot(r+1)\vec{a}_3-\omega t\right)\right)\\ =\left(\exp\left(i\left(pl\vec{k}\cdot\vec{a}_1+mq\vec{k}\cdot\vec{a}_2+nr\vec{k}\cdot\vec{a}_3\right)\right)\right)\left(\vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right)\right)\\ =\exp\left(i\left(pl\vec{k}\cdot\vec{a}_1+mq\vec{k}\cdot\vec{a}_2+nr\vec{k}\cdot\vec{a}_3\right)\right)\vec{u}_{lmn}.$$

The translation results in the same mode multiplied by a complex number. This shows that a normal mode of this form is an eigenfunction of the translation operator.

Remarkably, the phonon modes of any three-dimensional crystal have this form. What still needs to be determined is the vector $\vec{u}_{\vec{k}}$ which specifies the direction and the amplitude of the atomic motion for a particular mode. This vector can be determined by substituting the general normal mode solution into the classical equations of motion for a mass-spring system that models a crystal, where the masses are the atomic masses and the springs correspond to the linearized forces between the atoms.