When there are more atoms in the basis, Newton's laws consist of differential equations for the $x-$, $y-$, and $z-$motion of every atom. This is a total of $3p$ differential equations, where $p$ is the number of atoms in the basis. Because of translational symmetry, the normal mode solutions to these differential equations have the form,

$$\vec{u}_{lmn}^j = \vec{u}_{\vec{k}}^j\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right).$$

Here $j = 1,2,\cdots,p$ is an index that runs over the atoms in the basis. Inserting these solutions into the differential equations results in an eigenvalue problem that can be solved for $3p$ normal mode frequencies and $3p$ normal modes for each value of $\vec{k}$. Three of the normal modes are acoustic modes where $\omega \rightarrow 0$ as $|\vec{k}| \rightarrow 0$. The other $3p-3$ modes are optical modes where the normal mode frequencies are in the infrared for all values of $\vec{k}$.

As an example of a crystal with two atoms in the basis, consider NaCl.

Sodium chloride (NaCl) has an fcc Bravais lattice, and there are two atoms in the basis. The primitive lattice vectors are,

\begin{equation} \vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z}),\quad \vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y}),\quad\vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z}), \end{equation}

and the basis is Na (0,0,0) $j=1$ and Cl (0.5,0,0) $j=2$. Each Na atom has 6 nearest-neighbor Cl atoms and 12 next-nearest-neighbor Na atoms. Let $u^{1x}_{lmn}$ the displacement of Na atom in the unit cell at position $\vec{r}=l\vec{a}_1+m\vec{a}_2+n\vec{a}_3$ in the $x$-direction from its equilibrium position and $u^{2x}_{lmn}$ the displacement of Cl atom in the unit cell at position $\vec{r}=l\vec{a}_1+m\vec{a}_2+n\vec{a}_3$ in the $x$-direction from its equilibrium position. The restoring force that pushes the atoms back to their equilibrium positions is modelled with linear springs with spring constants $C_{\text{Na-Cl}}$, $C_{\text{Na-Na}}$, and $C_{\text{Cl-Cl}}$. These springs describe the interactions between the nearest-neighbor atoms and the next-nearest-neighbor atoms. Newton's laws for this case are,

\begin{equation} \begin{split} M_{\text{Na}} \frac {d^{2}u^{1x}_{lmn}}{dt^{2}} & = \frac{C_{\text{Na-Na}}}{2}\Big[ (u^{1x}_{(l+1)mn} - u^{1x}_{lmn})+ (u^{1x}_{(l-1)mn} - u^{1x}_{lmn})+ (u^{1x}_{l(m+1)n} - u^{1x}_{lmn}) + (u^{1x}_{l(m-1)n} - u^{1x}_{lmn})\\ & + (u^{1x}_{(l+1)m(n-1)} - u^{1x}_{lmn})+ (u^{1x}_{(l-1)m(n+1)} - u^{1x}_{lmn})+ (u^{1x}_{l(m+1)(n-1)} - u^{1x}_{lmn})+ (u^{1x}_{l(m-1)(n+1)}- u^{1x}_{lmn})\\ & + (u^{1y}_{l(m+1)n} - u^{1y}_{lmn}) + (u^{1y}_{l(m-1)n} - u^{1y}_{lmn}) - (u^{1y}_{(l+1)m(n-1)} - u^{1y}_{lmn}) - (u^{1y}_{(l-1)m(n+1)} - u^{1y}_{lmn})\\ &+ (u^{1z}_{(l+1)mn}- u^{1z}_{lmn})+ (u^{1z}_{(l-1)mn} - u^{1z}_{lmn})-(u^{1z}_{l(m+1)(n-1)} - u^{1z}_{lmn})- (u^{1z}_{l(m-1)(n+1)} - u^{1z}_{lmn})\Big] \\ &+C_{\text{Na-Cl}}\left( -2 u^{1x}_{lmn}+u^{2x}_{lmn}+u^{2x}_{(l-1)(m-1)(n+1)}\right), \end{split} \end{equation} \begin{equation} \begin{split} M_{\text{Na}} \frac {d^{2}u^{1y}_{lmn}}{dt^{2}} &= \frac{C_{\text{Na-Na}}}{2}\Big[ (u^{1y}_{l(m+1)n} - u^{1y}_{lmn}) + (u^{1y}_{l(m-1)n} - u^{1y}_{lmn}) + (u^{1y}_{(l+1)m(n-1)} - u^{1y}_{lmn})+ (u^{1y}_{(l-1)m(n+1)} - u^{1y}_{lmn}) \\ &+ (u^{1y}_{(l-1)(m+1)n} - u^{1y}_{lmn}) + (u^{1y}_{lm(n-1)} - u^{1y}_{lmn}) + (u^{1y}_{(l+1)(m-1)n} - u^{1y}_{lmn}) + (u^{1y}_{lm(n+1)} - u^{1y}_{lmn})\\ &+ (u^{1x}_{l(m+1)n} - u^{1x}_{lmn}) + (u^{1x}_{l(m-1)n} - u^{1x}_{lmn}) - (u^{1x}_{(l-1)m(n+1)} - u^{1x}_{lmn}) - (u^{1x}_{(l+1)m(n-1)} - u^{1x}_{lmn}) \\ &+ (u^{1z}_{lm(n-1)} - u^{1z}_{lmn})+(u^{1z}_{lm(n+1)} - u^{1z}_{lmn}) - (u^{1z}_{(l+1)(m-1)n} - u^{1z}_{lmn})- (u^{1z}_{(l-1)(m+1)n} - u^{1z}_{lmn}) \Big]\\ & +C_{\text{Na-Cl}}\left( -2 u^{1y}_{lmn}+u^{2y}_{(l-1)m(n+1)}+u^{2y}_{l(m-1)n}\right), \end{split} \end{equation} \begin{equation} \begin{split} M_{\text{Na}} \frac {d^{2}u^{1z}_{lmn}}{dt^{2}} &= \frac{C_{\text{Na-Na}}}{2}\Big[ (u^{1z}_{(l-1)mn} - u^{1z}_{lmn})+ (u^{1z}_{(l-1)l(m+1)n} - u^{1z}_{lmn})+ (u^{1z}_{l(m+1)(n-1)} - u^{1z}_{lmn}) + (u^{1z}_{lm(n-1)} - u^{1z}_{lmn}) \\ &+ (u^{1z}_{lm(n+1)} - u^{1z}_{lmn})+ (u^{1z}_{(l+1)mn} - u^{1z}_{lmn})+ (u^{1z}_{(l+1)(m-1)n} - u^{1z}_{lmn})+ (u^{1z}_{l(m-1)(n+1)} - u^{1z}_{lmn})\\ &+ (u^{1x}_{(l+1)mn} - u^{1x}_{lmn}) + (u^{1x}_{(l-1)mn} - u^{1x}_{lmn})-(u^{1x}_{l(m-1)(n+1)} - u^{1x}_{lmn}) - (u^{1x}_{l(m+1)(n-1)} - u^{1x}_{lmn})\\ &+(u^{1y}_{lm(n+1)} - u^{1y}_{lmn}) + (u^{1y}_{lm(n-1)} - u^{1y}_{lmn}) - (u^{1y}_{(l-1)(m+1)n} - u^{1y}_{lmn})- (u^{1y}_{(l+1)(m-1)n} - u^{1y}_{lmn})\Big]\\ &+ C_{\text{Na-Cl}}\left( -2 u^{1z}_{lmn}+u^{2z}_{(l-1)mn}+u^{2z}_{l(m-1)(n+1)}\right), \end{split} \end{equation} \begin{equation} \begin{split} M_{\text{Cl}} \frac {d^{2}u^{2x}_{lmn}}{dt^{2}} & = \frac{C_{\text{Cl-Cl}}}{2}\Big[ (u^{2x}_{(l+1)mn} - u^{2x}_{lmn})+ (u^{2x}_{(l-1)mn} - u^{2x}_{lmn})+ (u^{2x}_{l(m+1)n} - u^{2x}_{lmn}) + (u^{2x}_{l(m-1)n} - u^{2x}_{lmn})\\ & + (u^{2x}_{(l+1)m(n-1)} - u^{2x}_{lmn})+ (u^{2x}_{(l-1)m(n+1)} - u^{2x}_{lmn})+ (u^{2x}_{l(m+1)(n-1)} - u^{2x}_{lmn})+ (u^{2x}_{l(m-1)(n+1)}- u^{2x}_{lmn})\\ & + (u^{2y}_{l(m+1)n} - u^{2y}_{lmn}) + (u^{2y}_{l(m-1)n} - u^{2y}_{lmn}) - (u^{2y}_{(l+1)m(n-1)} - u^{2y}_{lmn}) - (u^{2y}_{(l-1)m(n+1)} - u^{2y}_{lmn})\\ &+ (u^{2z}_{(l+1)mn}- u^{2z}_{lmn})+ (u^{2z}_{(l-1)mn} - u^{2z}_{lmn})-(u^{2z}_{l(m+1)(n-1)} - u^{2z}_{lmn})- (u^{2z}_{l(m-1)(n+1)} - u^{2z}_{lmn})\Big] \\ &+C_{\text{Na-Cl}}\left( -2 u^{2x}_{lmn}+u^{1x}_{lmn}+u^{1x}_{(l+1)(m+1)(n-1)}\right), \end{split} \end{equation} \begin{equation} \begin{split} M_{\text{Cl}} \frac {d^{2}u^{2y}_{lmn}}{dt^{2}} &= \frac{C_{\text{Cl-Cl}}}{2}\Big[ (u^{2y}_{l(m+1)n} - u^{2y}_{lmn}) + (u^{2y}_{l(m-1)n} - u^{2y}_{lmn}) + (u^{2y}_{(l+1)m(n-1)} - u^{2y}_{lmn})+ (u^{2y}_{(l-1)m(n+1)} - u^{2y}_{lmn}) \\ &+ (u^{2y}_{(l-1)(m+1)n} - u^{2y}_{lmn}) + (u^{2y}_{lm(n-1)} - u^{2y}_{lmn}) + (u^{2y}_{(l+1)(m-1)n} - u^{2y}_{lmn}) + (u^{2y}_{lm(n+1)} - u^{2y}_{lmn})\\ &+ (u^{2x}_{l(m+1)n} - u^{2x}_{lmn}) + (u^{2x}_{l(m-1)n} - u^{2x}_{lmn}) - (u^{2x}_{(l-1)m(n+1)} - u^{2x}_{lmn}) - (u^{2x}_{(l+1)m(n-1)} - u^{2x}_{lmn}) \\ &+ (u^{2z}_{lm(n-1)} - u^{2z}_{lmn})+(u^{2z}_{lm(n+1)} - u^{2z}_{lmn}) - (u^{2z}_{(l+1)(m-1)n} - u^{2z}_{lmn})- (u^{2z}_{(l-1)(m+1)n} - u^{2z}_{lmn}) \Big]\\ &+ C_{\text{Na-Cl}}\left( -2 u^{2y}_{lmn}+u^{1y}_{l(m+1)n}+u^{1y}_{(l+1)m(n-1)}\right), \end{split} \end{equation} \begin{equation} \begin{split} M_{\text{Cl}} \frac {d^{2}u^{2z}_{lmn}}{dt^{2}} &= \frac{C_{\text{Cl-Cl}}}{2}\Big[ (u^{2z}_{(l-1)mn} - u^{2z}_{lmn})+ (u^{2z}_{(l-1)l(m+1)n} - u^{2z}_{lmn})+ (u^{2z}_{l(m+1)(n-1)} - u^{2z}_{lmn}) + (u^{2z}_{lm(n-1)} - u^{2z}_{lmn}) \\ &+ (u^{2z}_{lm(n+1)} - u^{2z}_{lmn})+ (u^{2z}_{(l+1)mn} - u^{2z}_{lmn})+ (u^{2z}_{(l+1)(m-1)n} - u^{2z}_{lmn})+ (u^{2z}_{l(m-1)(n+1)} - u^{2z}_{lmn})\\ &+ (u^{2x}_{(l+1)mn} - u^{2x}_{lmn}) + (u^{2x}_{(l-1)mn} - u^{2x}_{lmn})-(u^{2x}_{l(m-1)(n+1)} - u^{2x}_{lmn}) - (u^{2x}_{l(m+1)(n-1)} - u^{2x}_{lmn})\\ &+(u^{2y}_{lm(n+1)} - u^{2y}_{lmn}) + (u^{2y}_{lm(n-1)} - u^{2y}_{lmn}) - (u^{2y}_{(l-1)(m+1)n} - u^{2y}_{lmn})- (u^{2y}_{(l+1)(m-1)n} - u^{2y}_{lmn})\Big]\\ &+ C_{\text{Na-Cl}}\left( -2 u^{2z}_{lmn}+u^{1z}_{l(m+1)(n-1)}+u^{1z}_{(l+1)mn}\right). \end{split} \end{equation}

The next-nearest neighbors are on an fcc lattice, so the form for the next-nearest-neighbor spring forces was copied from the fcc page. By substituting the form for the normal modes given above into the differential equation, the following dispersion relation can be calculated.

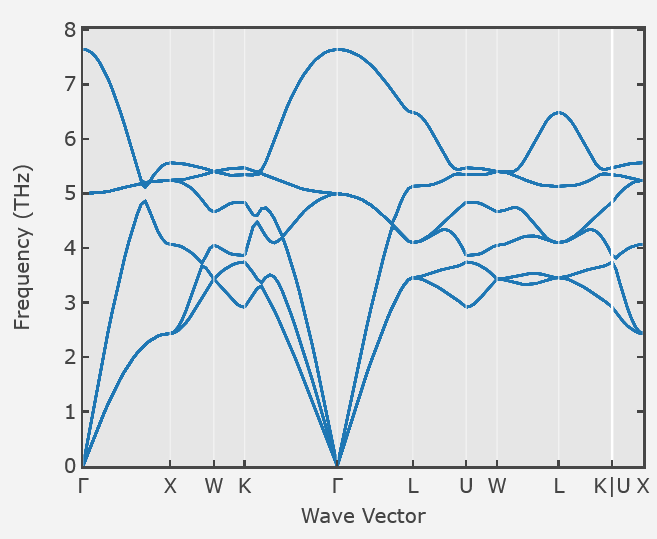
Source: Materials Project mp-22862

For NaCl, there are six normal modes for every value of $\vec{k}$. There are three acoustic branches the the dispersion relation, with one longitudinal branch and two transverse branches. Of the three optical modes, one is longitudinal and two are transverse. In some directions, such as $\Gamma - X$, the two transverse modes have the same frequency because of symmetry.

The phonon density of states can be calculated using the same equations. Choose an equally spaced grid of $\vec{k}$ values in the first Brillouin zone. For every $\vec{k}$, solve for the $3p$ frequencies and make a histogram of the number of times a particular frequency appears as a function of frequency. The total number of normal modes is three times the number of atoms in the crystal, so the integral of the density of states over all frequencies will be three times the number of atoms in a crystal. The number of normal modes depends on the size of the crystal, so the density of states is calculated per cubic meter.