The phonon dispersion relation for fcc can be calculated by modelling the crystal as a lattice of equal masses connected by linear springs. The masses are the atomic masses and the spring constants are obtained by linearizing the atomic forces between the atoms. For fcc, the primitive lattice vectors are,

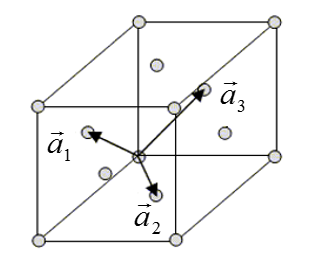$$\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z}),$$ $$\vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y}),$$ $$\vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z}).$$

Consider an fcc crystal with one atom in the basis. Let $u^x_{lmn}$ the displacement the atom in the unit cell at position $\vec{r}=l\vec{a}_1+m\vec{a}_2+n\vec{a}_3$ in the $x$-direction from its equilibrium position. If the restoring force that pushes the atoms back to their equilibrium positions is modelled with a linear spring with spring constants $C$, the equations of motion in this case are,

\begin{equation} \begin{split} M \frac {d^{2}u^{x}_{lmn}}{dt^{2}} & = \frac{C}{2}\Big[ (u^{x}_{(l+1)mn} - u^{x}_{lmn})+ (u^{x}_{(l-1)mn} - u^{x}_{lmn})+ (u^{x}_{l(m+1)n} - u^{x}_{lmn}) + (u^{x}_{l(m-1)n} - u^{x}_{lmn})\\ & + (u^{x}_{(l+1)m(n-1)} - u^{x}_{lmn})+ (u^{x}_{(l-1)m(n+1)} - u^{x}_{lmn})+ (u^{x}_{l(m+1)(n-1)} - u^{x}_{lmn})+ (u^{x}_{l(m-1)(n+1)}- u^{x}_{lmn})\\ & + (u^{y}_{l(m+1)n} - u^{y}_{lmn}) + (u^{y}_{l(m-1)n} - u^{y}_{lmn}) - (u^{y}_{(l+1)m(n-1)} - u^{y}_{lmn}) - (u^{y}_{(l-1)m(n+1)} - u^{y}_{lmn})\\ &+ (u^{z}_{(l+1)mn}- u^{z}_{lmn})+ (u^{z}_{(l-1)mn} - u^{z}_{lmn})-(u^{z}_{l(m+1)(n-1)} - u^{z}_{lmn})- (u^{z}_{l(m-1)(n+1)} - u^{z}_{lmn})\Big], \end{split} \end{equation} \begin{equation} \begin{split} M \frac {d^{2}u^{y}_{lmn}}{dt^{2}} &= \frac{C}{2}\Big[ (u^{y}_{l(m+1)n} - u^{y}_{lmn}) + (u^{y}_{l(m-1)n} - u^{y}_{lmn}) + (u^{y}_{(l+1)m(n-1)} - u^{y}_{lmn})+ (u^{y}_{(l-1)m(n+1)} - u^{y}_{lmn}) \\ &+ (u^{y}_{(l-1)(m+1)n} - u^{y}_{lmn}) + (u^{y}_{lm(n-1)} - u^{y}_{lmn}) + (u^{y}_{(l+1)(m-1)n} - u^{y}_{lmn}) + (u^{y}_{lm(n+1)} - u^{y}_{lmn})\\ &+ (u^{x}_{l(m+1)n} - u^{x}_{lmn}) + (u^{x}_{l(m-1)n} - u^{x}_{lmn}) - (u^{x}_{(l-1)m(n+1)} - u^{x}_{lmn}) - (u^{x}_{(l+1)m(n-1)} - u^{x}_{lmn}) \\ &+ (u^{z}_{lm(n-1)} - u^{z}_{lmn})+(u^{z}_{lm(n+1)} - u^{z}_{lmn}) - (u^{z}_{(l+1)(m-1)n} - u^{z}_{lmn})- (u^{z}_{(l-1)(m+1)n} - u^{z}_{lmn}) \Big], \end{split} \end{equation} \begin{equation} \begin{split} M \frac {d^{2}u^{z}_{lmn}}{dt^{2}} &= \frac{C}{2}\Big[ (u^{z}_{(l-1)mn} - u^{z}_{lmn})+ (u^{z}_{(l-1)l(m+1)n} - u^{z}_{lmn})+ (u^{z}_{l(m+1)(n-1)} - u^{z}_{lmn}) + (u^{z}_{lm(n-1)} - u^{z}_{lmn}) \\ &+ (u^{z}_{lm(n+1)} - u^{z}_{lmn})+ (u^{z}_{(l+1)mn} - u^{z}_{lmn})+ (u^{z}_{(l+1)(m-1)n} - u^{z}_{lmn})+ (u^{z}_{l(m-1)(n+1)} - u^{z}_{lmn})\\ &+ (u^{x}_{(l+1)mn} - u^{x}_{lmn}) + (u^{x}_{(l-1)mn} - u^{x}_{lmn})-(u^{x}_{l(m-1)(n+1)} - u^{x}_{lmn}) - (u^{x}_{l(m+1)(n-1)} - u^{x}_{lmn})\\ &+(u^{y}_{lm(n+1)} - u^{y}_{lmn}) + (u^{y}_{lm(n-1)} - u^{y}_{lmn}) - (u^{y}_{(l-1)(m+1)n} - u^{y}_{lmn})- (u^{y}_{(l+1)(m-1)n} - u^{y}_{lmn})\Big]. \end{split} \end{equation}

The general solution of the normal modes of this crystal is required by symmetry to be,

$$\vec{u}_{lmn} = \vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right)=\vec{u}_{\vec{k}}\exp\left(i\frac{l+m}{2}k_xa\right)\exp\left(i\frac{m+n}{2}k_ya\right)\exp\left(i\frac{l+n}{2}k_za\right).$$

Substituting this solution into the differential equations above results in the following algebraic equations,

\begin{equation} \begin{split} -\omega^2M u^{x}_{\vec{k}} & = \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} + e^{i(k_xa/2-k_ya/2)} + e^{-i(k_xa/2-k_ya/2)} + e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} + e^{i(k_xa/2-k_za/2)} + e^{-i(k_xa/2-k_za/2)} - 8 \Big] u^{x}_{\vec{k}}\\ & + \frac{C}{2}\Big[ e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} - e^{i(k_xa/2-k_ya/2)} - e^{-i(k_xa/2-k_ya/2)} \Big] u^{y}_{\vec{k}}\\ &+ \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} - e^{i(k_xa/2-k_za/2)} - e^{-i(k_xa/2-k_za/2)}\Big] u^{z}_{\vec{k}}, \end{split} \end{equation} \begin{equation} \begin{split} -\omega^2M u^{y}_{\vec{k}} &= \frac{C}{2}\Big[ e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} - e^{i(k_xa/2-k_ya/2)} - e^{-i(k_xa/2-k_ya/2)} \Big] u^{x}_{\vec{k}}\\ &+ \frac{C}{2}\Big[e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} + e^{i(k_xa/2-k_ya/2)} + e^{-i(k_xa/2-k_ya/2)} + e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} + e^{i(k_ya/2-k_za/2)} + e^{-i(k_ya/2-k_za/2)} - 8 \Big] u^{y}_{\vec{k}}\\ &+ \frac{C}{2}\Big[ e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} - e^{i(k_ya/2-k_za/2)} - e^{-i(k_ya/2-k_za/2)}\Big] u^{z}_{\vec{k}}, \end{split} \end{equation} \begin{equation} \begin{split} -\omega^2M u^{z}_{\vec{k}} & = \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} - e^{i(k_xa/2-k_za/2)} - e^{-i(k_xa/2-k_za/2)}\Big] u^{x}_{\vec{k}}\\ & + \frac{C}{2}\Big[ e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} - e^{i(k_ya/2-k_za/2)} - e^{-i(k_ya/2-k_za/2)} \Big] u^{y}_{\vec{k}}\\ & + \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} + e^{i(k_ya/2-k_za/2)} + e^{-i(k_ya/2-k_za/2)} + e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} + e^{i(k_xa/2-k_za/2)} + e^{-i(k_xa/2-k_za/2)} - 8 \Big] u^{z}_{\vec{k}}\\ \end{split} \end{equation}

Using the identity $e^{i\theta}+e^{-i\theta}=2\cos(\theta)$, these equations can be written as an eigenvalue problem,

\begin{equation} \left[ \begin{array}{c} 4 - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) & - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) & - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) \\ - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) & 4 - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) - \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) & - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) \\ - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) & - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) & 4 - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) - \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) \end{array} \right] \left[ \begin{array}{b} u_{\vec{k}}^x \\ u_{\vec{k}}^y \\ u_{\vec{k}}^z \end{array} \right]=\frac{M\omega^2}{C} \left[ \begin{array}{b} u_{\vec{k}}^x \\ u_{\vec{k}}^y \\ u_{\vec{k}}^z \end{array} \right] \end{equation}

The solutions to these equations can be found by setting the determinant of the matrix equal to zero.