One of the remarkable papers that Einstein published in 1905 was about Brownian motion. In it, he considered what happens to particles confined to a region of space by a potential $U$. The force on the particles will be $\vec{F}=-\nabla U$ and they will be pulled to this minimum of the potential. This will cause a high concentration of particles at the minimum, and they will diffuse away from the minimum. In equilibrium, there must be a balance between the inward current due to the attractive potential and the outward current due to diffusion.

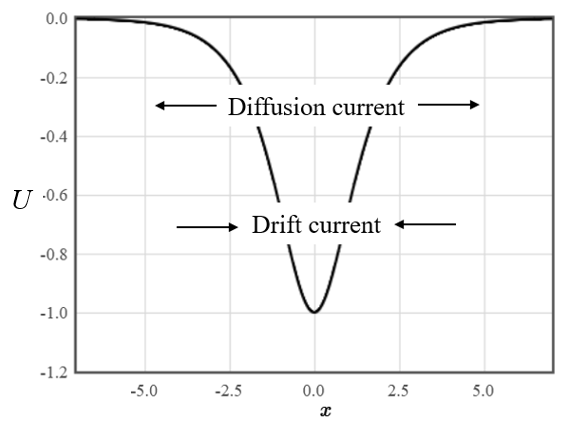
If the particles are electrons, the potential will be $U=-eV$ where $V$ is the electrostatic potential, the drift current density pulling the electrons to the minimum will be $j_{\text{drift}} = ne\mu_e \vec{E}$ and the diffusion current density pushing them away from the minimum will be $j_{\text{diffusion}}=eD\nabla n$, so the total current density is,

$$\vec{j} = ne\mu_e\vec{E} + eD\nabla n.$$

Since the current density must be zero in equilibrium, we have,

$$n\mu_e\vec{E} = -D\nabla n.$$

Einstein used Boltzmann's theory to argue that the electron density should be described by a Boltzmann factor,

$$n = n_0\exp\left(\frac{-U}{k_BT}\right)= n_0\exp\left(\frac{eV}{k_BT}\right).$$

The gradient of the electron density would then be,

$$\nabla n = \frac{n_0e}{k_BT}\nabla V\exp\left(\frac{eV}{k_BT}\right)= \frac{e\nabla V}{k_BT}n.$$

Substituting this into the equation for the balance between the drift and diffusion currents and using the fact that $\vec{E}=-\nabla V$ yields,

$$\bbox[10px, border: 1px solid black]{\mu_e = \frac{eD}{k_BT}.}$$

This is known as the Einstein relation. It says that particles with a high diffusion constant will have a high mobility.

---

• A. Einstein, Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Annalen der Physik (1905).