For powder diffraction, a crystal is ground into a fine powder so that there are many small crystals with random orientations. X-rays strike the surface of the sample at an angle θ and an x-ray detector is placed at an angle θ to the surface. Only planes parallel to the surface will diffract x-rays to the detector.

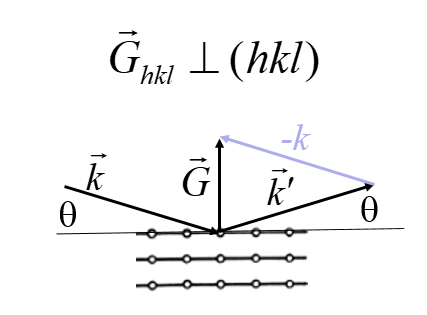
Since there are many small crystals with random orientations in the sample, all possible crystal planes that can diffract the x-rays will contribute to the measured signal when θ satisifies the Bragg condition. The form below can calculate the powder diffraction pattern for any crystal with up to five atoms per primitive unit cell. Some buttons are provided that load the form with the data for certain crystals. Here is further discussion of powder diffraction.

I  2θ

Primitive lattice vectors:  $\vec{a}_1=$ $\hat{x}+$ $\hat{y}+$ $\hat{z}$ [m]   $\vec{a}_2=$ $\hat{x}+$ $\hat{y}+$ $\hat{z}$ [m]  $\vec{a}_3=$ $\hat{x}+$ $\hat{y}+$ $\hat{z}$ [m]  Basis:  The positions of the atoms are given in fractional coodinates between -1 and 1. $\vec{a}_1+$  $\vec{a}_2+$  $\vec{a}_3$  $\vec{a}_1+$  $\vec{a}_2+$  $\vec{a}_3$  $\vec{a}_1+$  $\vec{a}_2+$  $\vec{a}_3$  $\vec{a}_1+$  $\vec{a}_2+$  $\vec{a}_3$  $\vec{a}_1+$  $\vec{a}_2+$  $\vec{a}_3$  X-ray wavelength λ [Å] = 1.540598 Cu Kα 2.28975 Cr Kα 0.7093165 Mo Kα

Primitive reciprocal lattice vectors

$\vec{b}_1=2\pi\frac{\vec{a}_2\times\vec{a}_3}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1]

$\vec{b}_2=2\pi\frac{\vec{a}_3\times\vec{a}_1}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1]

$\vec{b}_3=2\pi\frac{\vec{a}_1\times\vec{a}_2}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1]

The script first calculates the primitive reciprocal lattice vectors from the primitive lattice vectors in real space. Then for each reciprocal lattice vector $\vec{G} = h\vec{b}_1+k\vec{b}_2+l\vec{b}_3$, the structure factor $n_{\vec{G}}$ is calculated. All reciprocal lattice vectors with the same absolute value diffract x-rays at the same angle. In the table below, $N$ is the number of reciprocal lattice vectors that have contribute to the diffraction signal for a certain angle θ. $d_{hkl} = 2\pi/|\vec{G}_{hkl}|$ is the distance between the $hkl$ netplanes.

Structure factors

$G_{hkl}$ Å-1

$d_{hkl}$ Å

$2\theta$

$|n_{\vec{G}}|$

$I=N|n_{\vec{G}}|^2$

$N$