PHY.K02UF Molecular and Solid State Physics
|
| |||
PHY.K02UF Molecular and Solid State Physics | ||||
Everything there is to know about the properties of a solid can be deduced from how the atoms are arranged. It is easiest to specify where all of the atoms are in a solid if the atoms are arranged in a periodic pattern and align in straight rows. This is known as a crystal. Much of our understanding of solids, even non-crystalline solids, comes from studying crystals. Common crystals are sugar crystals, iron, salt crystals, gold, silicon, quartz crystals, diamonds, copper, and rubies. Metals, semiconductors, insulators, and (biological) molecules will form crystals. Crystals often form beautiful geometric shapes because when the atoms are arranged periodically, they break more easily at certain planes.
|
|
|
|
|
|
diamond |
gallium (a metal) |
ruby |
insulin |
rose quartz |
sugar |
A small part of a crystal that can be repeated to form the entire crystal is called a unit cell. A primitive unit cell is the smallest unit that can be repeated periodically to form a crystal. The atoms in the primitive unit cell are called the basis of the crystal. The basis has to have the same chemical composition as the crystal. For some crystals, such as copper or gold, the basis consists of just one atom; however, in a sugar crystal, the basis consists of all 45 atoms in a sucrose molecule.
Primitive unit cell | Crystal |
|  |
copper | |
|  |
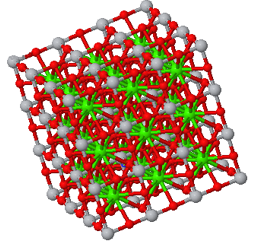CaTiO3 | |
|  |
sugar | |
For every crystal structure, a three-dimensional periodic lattice of points called a Bravais lattice can be found. By repeating a primitive unit cell at every Bravais lattice point, the entire crystal can be constructed. Every Bravais lattice point is equivalent; the environment of any Bravais lattice point is the same as that of every other Bravais lattice point. Given a Bravais lattice, primitive unit vectors $\vec{a}_1$, $\vec{a}_2$, $\vec{a}_3$, that connect neighboring Bravais lattice points can be found. The translation vector from one Bravais lattice point to another is,
$$\vec{T}_{uvw} = u\vec{a}_1 + v\vec{a}_2 + w\vec{a}_3.$$Here $u$, $v$, $w$, are positive or negative integers. The atoms of the basis are repeated at every point in the lattice to form the crystal. For a given Bravais lattice, the choice of primitive lattice vectors is not unique. Three choices of primitive lattice vectors are shown below for a two-dimensional Bravais lattice.
While primitive lattice vectors are not unique, the volume associated with every Bravais lattice point does not depend on the choice of primitive lattice vectors. In two dimensions, there are 5 Bravais lattices and the area of the primitive unit cell is $\vec{a}_1 \times \vec{a}_2$. In three dimensions, there are 14 Bravais lattices, and the volume of the primitive unit cell is $\vec{a}_1\cdot(\vec{a}_2 \times \vec{a}_3)$. The 14 Bravais lattices in three dimensions are divided into 7 crystal systems: cubic, hexagonal, rhombohedral = trigonal, tetragonal, orthorhombic, monoclinic, and triclinic. The conventional unit cell for each crystal system is a parallelopiped with 8 corners and 6 faces. The three edges of the unit cell have lengths $a$, $b$, and $c$. The angles are defined as $\alpha$ is the angle between $b$ and $c$, $\beta$ is the angle between $a$ and $c$, and $\gamma$ is the angle between $a$ and $b$.
There is a special primitive unit cell, called a Wigner-Seitz cell, that has the maximum symmetry for a given Bravais lattice. A Wigner-Seitz cell is constructed by choosing a Bravais lattice point (they are all equivalent) and drawing a line from that Bravais lattice point to all surrounding Bravais lattice points. Then, planes are drawn that bisect these lines. The volume that can be reached from the chosen Bravais lattice point without crossing any of the planes is the Wigner-Seitz cell. Wigner-Seitz cells can be packed together to fill space without any gaps in between them.
There are apps to draw the Wigner-Seitz cells in two dimensions and three dimensions.
The 14 Bravais lattices are divided into the 7 crystal systems, which are explained below.
Cubic: For a cubic crystal, $a = b=c$ and $\alpha = \beta = \gamma = 90^{\circ}$. A crystal is considered cubic if a cubic unit cell can be found, even if the primitive unit cell is not cubic. There are three Bravais lattices in the cubic crystal system: simple cubic (sc), body-centered cubic (bcc), and face-centered cubic (fcc).
 |
 |
 | ||
| Simple cubic (cP) | Body-centered cubic (cI) | Face-centered cubic (cF) |
For simple cubic, the primitive unit cell is a cube, and it is the same as the conventional unit cell. There is a Bravais lattice point in each corner of the cube and each corner is shared by 8 cubes, so there are ($8\times \frac{1}{8} = 1$) Bravais lattice points per unit cell. The volume of the primitive unit cell is $a^3$. The Wigner-Seitz cell is also a cube with a volume $a^3$. For bcc, there are two Bravais lattice points in the conventional unit cell; one at the body center of the cube and one shared by the 8 corners. The (primitive) Wigner-Seitz cell of a bcc lattice can be constructed by bisecting the lines from a Bravais lattice point to its 8 nearest neighbors and 6 next-nearest neighbors. The resulting Wigner-Seitz cell contains one Bravais lattice point, has a volume of $\frac{a^3}{2}$, and has the shape of a truncated octahedron. For fcc, there are four Bravais lattice points in the conventional unit cell, ($8\times \frac{1}{8} = 1$) at the corners and ($6\times \frac{1}{2} = 3$) on the faces. Each fcc Bravais lattice point has 12 nearest neighbors, and the Wigner-Seitz cell of an fcc Bravais lattice is a rhombic dodecahedron with a volume of $\frac{a^3}{4}$.
|
|
| ||
| sc Wigner-Seitz cell cube | bcc Wigner-Seitz cell truncated octahedron | fcc Wigner-Seitz cell rhombic dodecahedron |
If equally sized spheres are stacked in a simple cubic pattern so that they are touching each other, each sphere touches 6 neighbors, and the fraction of the total volume occupied by the spheres is 52%. This is called the packing density. If equally sized spheres are stacked in a body-centered cubic pattern so that they are touching each other, each sphere touches 8 neighbors, and the fraction of the total volume occupied by the spheres is 68%. If equally sized spheres are stacked in a face-centered cubic pattern so that they are touching each other, each sphere touches 12 neighbors, and the fraction of the total volume occupied by the spheres is 74%. If equally sized spheres are poured into a container so that they arrange randomly while touching each other, the packing density is about 64%. This is called random close pack.
Hexagonal: For a hexagonal crystal, $a = b\ne c$ and $\alpha = \beta = 90^{\circ}$, $\gamma = 120^{\circ}$. The crystalographic unit cell is shown on the left. The base is a rhombus with angles of 60° and 120°. A three times larger conventional unit cell with hexagonal symmetry is shown on the right.
 |
 | |
| Unit cell with rhombus base (hP) | Hexagonal unit cell |
The Wigner-Seitz cell is a hexagonal cylinder with the volume of the conventional unit cell $\vec{a}_1\cdot(\vec{a}_2 \times \vec{a}_3) = \frac{\sqrt{3}}{2} a^2c$.
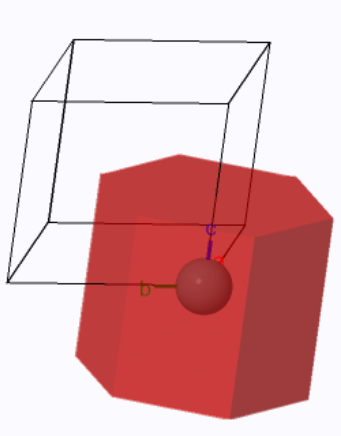
The Wigner-Seitz cell (red) and the conventional unit cell.
Rhombohedral = Trigonal: The rhombohedral crystal system is sometimes called the trigonal crystal system. For this crystal system, $a = b = c$ and $\alpha = \beta = \gamma \ne 90^{\circ}$. To create a rhombohedral unit cell, you can start with a cube and deform it by pushing from a corner in the direction of the center of the cube. All of the sides will stay the same length, but the angles will no longer be 90°. In geometry, this shape is called a rhombohedron.
Rhombohedral (hR)
The Wigner-Seitz cell of a rhombohedral Bravais lattice typically has 14 sides. There are 6 four-sided faces (from the planes that bisect the lines to the 6 nearest neighbors) and 8 six-sided faces (from the planes that bisect the lines to the 8 next-nearest neighbors).
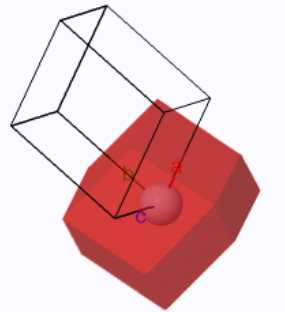
The Wigner-Seitz cell (red) and the conventional unit cell.
Tetragonal: For a tetragonal crystal, $a = b \ne c$ and $\alpha = \beta = \gamma = 90^{\circ}$. A crystal is considered tetragonal if a tetragonal unit cell can be found, even if the primitive unit cell is not tetragonal. There are two tetragonal Bravais lattices.
 |
 | ||
| Simple tetragonal (tP) | Body-centered tetragonal (tI) |
For simple tetragonal, the primitive unit cell is the same as the conventional unit cell and the Wigner-Seitz cell. It is a rectangular solid with a square base and has a volume of $a^2c$. For the body-centered tetragonal Bravais lattice, there are two Bravais lattice points in the conventional unit cell, so the volume of the primitive unit cell is $\frac{1}{2}a^2c$. The Wigner-Seitz cell of a body-centered tetragonal Bravais lattice has 8 six-sided faces (from the planes that bisect the lines to the 8 nearest neighbors) and 6 four-sided faces (from the planes that bisect the lines to the next-nearest neighbors).
 |
 | ||
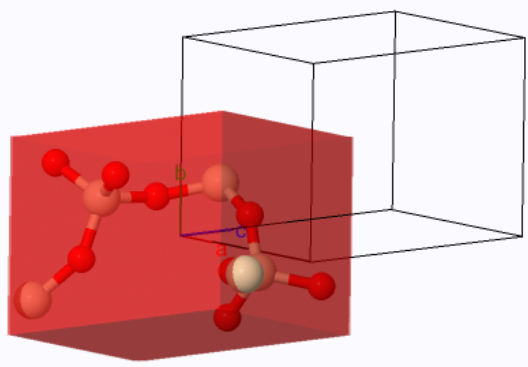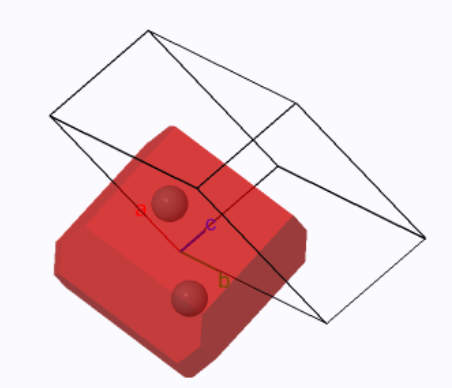| The simple tetragonal Wigner-Seitz cell (red) and the primitive unit cell (black outline). | The body-centered tetragonal Wigner-Seitz cell (red) and the primitive unit cell (black outline). |
Orthorhombic: For a orthorhombic crystal, $a \ne b \ne c$ and $\alpha = \beta = \gamma = 90^{\circ}$. A crystal is considered orthogonal if a orthogonal unit cell can be found, even if the primitive unit cell is not orthogonal. There are four Bravais lattices in the orhtorhomic crystal system: simple orthorhomic, base-centered orthorhomic, body-centered orthorhomic, and face-centered orthorhomic.
 |
 |
 |
 | ||||
| Simple orthorhombic (oP) | Base-centered orthorhombic (oS) | Body-centered orthorhombic (oI) | Face-centered orthorhombic (oF) |
For simple orthorhombic, the primitive unit cell is the same as the conventional unit cell and the Wigner-Seitz cell. It is a rectangular prism with 6 faces. The volume of the primitive unit cell is $abc$. For the base-centered orthorhombic Bravais lattice, there are two Bravais lattice points in the conventional unit cell, and the primitive unit cell has half of the volume of the conventional unit cell $\frac{abc}{2}$. The Wigner-Seitz cell typically has 2 six-sided faces and 6 four-sided faces, but the shape can be different depending on the ratio of the lattice parameters $a$, $b$, and $c$. For body-centered orthorhombic Bravais lattice, there are two Bravais lattice points in the conventional unit cell, and the primitive unit cell has half of the volume of the conventional unit cell $\frac{abc}{2}$. For face-centered orthorhombic, there are four Bravais lattice points in the conventional unit cell, and the primitive unit cell has one quarter of the volume of the conventional unit cell $\frac{abc}{4}$. The Wigner-Seitz cell for the body-centered and the face-centered Bravais lattices typically have 8 six-sided faces and 6 four-sided faces but the shape can be different depending on the ratio of the lattice parameters $a$, $b$, and $c$.
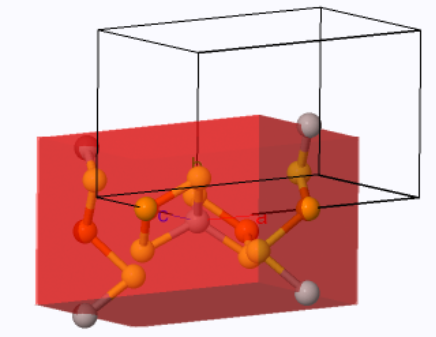 The simple orthorhombic Wigner-Seitz cell (red) and the primitive unit cell (black outline). |
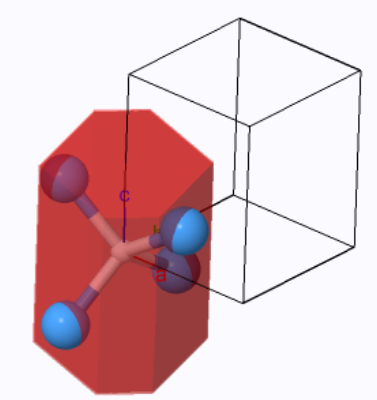 The base-centered orthorhombic Wigner-Seitz cell (red) and the primitive unit cell (black outline). | |
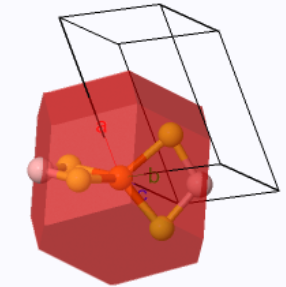 The body-centered orthorhombic Wigner-Seitz cell (red) and the primitive unit cell (black outline). |
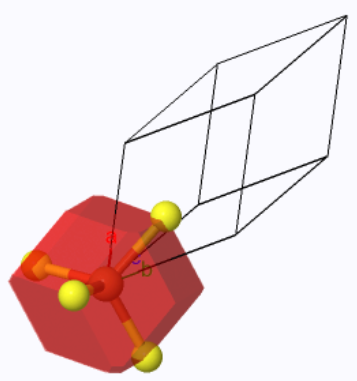 The face-centered tetragonal Wigner-Seitz cell (red) and the primitive unit cell (black outline). |
Monoclinic: For monoclinic crystals, $a \ne b \ne c$ and $\alpha \ne 90^{\circ}, \beta = \gamma = 90^{\circ}$. To generate a monoclinic unit cell, start with an orthorhombic unit cell and push on one of the faces so that the angles at the base of the unit cell remain $90^{\circ}$, but one angle is not $90^{\circ}$.
 |
 | ||
| Simple monoclinic (mP) | Base-centered monoclinic (mS) |
Triclinic: Triclinic cystals have the least symmetry. For this crystal system, $a \ne b \ne c$ and $\alpha \ne \beta \ne \gamma $.
Triclinic (aP)
A triclinic Bravais can be nearly the same as any of the other Bravais lattices. Consequently, the Wigner-Seitz cell can have many different shapes depending on the lattice parameters.
Crystals are classified into Bravais lattices using Pearson symbols. The Pearson symbol consists of a two-letter combination that specifies the Bravais lattice and a number which specifies the number of atoms in the conventional unit cell. The first letter specifies the crystal system, and the second letter the Bravais lattice of that crystal system.
| Crystal system | Pearson Notation | |
| a - Triclinic | aP - Triclinic | |
| m - Monoclinic | mP - Simple monoclinic | |
| o - Orthorhombic | mS - Base-centered monoclinic | |
| t - Tetragonal | oP - Simple orthorhombic | |
| h - Hexagonal | oS - Base-centered orthorhombic | |
| c - Cubic | oI - Body-centered orthorhombic | |
| oF - Face-centered orthorhombic | ||
| Lattice type | tP - Simple tetragonal | |
| P - Primitive | tI - Body-centered tetragonal | |
| I - Body centered | hR - Rhombohedral | |
| F - Face centered | hP - Hexagonal | |
| R - Rhombohedral | cF - Face-centered cubic | |
| S - Centered | cI - Body-centered cubic | |
| cP - Simple cubic |
For the centered Bravais lattices (mS and oS), sometimes A, B, or C replaces the S. The symbol oA means the centered plane cuts the $x-$axis, oB means the centered plane cuts the $y-$axis, and oC means the centered plane cuts the $z-$axis.
Copper has an fcc Bravais lattice, and there is one atom in the basis and one atom in the conventional unit cell. The Pearson symbol for copper is cF1. Iron has a bcc Bravais lattice, and there is one atom in the basis but two atoms in the conventional unit cell. The Pearson symbol for iron is cI2. Diamond has an fcc Bravais lattice with two atoms in the basis. There are therefore 8 atoms in the conventional unit cell, and the Pearson symbol for diamond is cF8. Different crystal structures can have the same Pearson symbol. A catalog of crystal structures sorted by their Pearson symbols can be found in the Encyclopedia of Crystallographic Prototypes.
Sometimes it is necessary to specify a direction in a crystal. Instead of using orthogonal coordinate axes $x$, $y$, and $z$, it is often more convenient to choose coordinate axes that align with the directions where the atoms are in straight rows in the crystal. This is done by defining the directions in terms of the lattice vectors. Any direction in a crystal can be specified by a translation vector of the form,
\[ \begin{equation} \vec{T}_{uvw} = u\vec{a}_1 + v\vec{a}_2 + w\vec{a}_3, \end{equation} \]where $\vec{a}_1$, $\vec{a}_2$, $\vec{a}_3$ are the lattice vectors and $u$, $v$, and $w$ are integers. The direction that the vector $\vec{T}_{uvw}$ points is denoted with square brackets, $[uvw]$. In a cubic system, the $x-$direction is $[100]$, the $y-$direction is $[010]$, and the $z-$direction is $[001]$. The $[110]$ direction is along the diagonal of a face of a cube, and the $[111]$ direction is the body diagonal of a cube.
 |  |  |
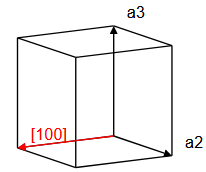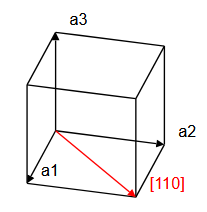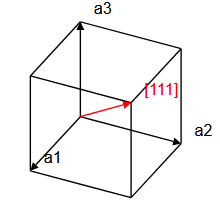If there are directions that are equivalent due to symmetry, any of the equivalent directions are specified by angular brackets <$hkl$>.
For example, in a cubic system:
<100> = [100], [010], [001], [-100], [0-10], [00-1]
<110> = [110], [-1-10], [1-10], [-110], [101], [-10-1], [-101], [10-1], [011], [0-1-1], [0-11], [01-1].
Often the minus signs are drawn as overlines [-10-1] = $\left[\overline{1}0\overline{1}\right]$. This is sometimes pronounced one-bar zero one-bar. If $u$,$v$, and $w$ have a common denominator, it is customary to divide by the common denominator when specifying a direction with Miller indices.
Planes are denoted with curved brackets $(hkl)$ where $h$, $k$, and $l$ are integers calle Miller indices. For cubic crystals, the $(hkl)$ plane is normal to the $[hkl]$ direction. However, this simple relationship does not hold for the other crystal systems.
Generally, the $(hkl)$ plane intercepts the axis in the direction of $\vec{a}_1$ at $\frac{|\vec{a}_1|}{h}$, the axis in the direction of $\vec{a}_2$ at $\frac{|\vec{a}_2|}{k}$, and the axis in the direction of $\vec{a}_3$ at $\frac{|\vec{a}_3|}{l}$. This definition results in planes (called net planes) where the atoms are arranged in periodic two-dimensional patterns. A crystal can be though of as a stacking of net planes.
Equivalent planes are denoted with curly brackets $\{hkl\}$. Three points that can be used to define the $(hkl)$ plane are $\left( \frac{a_{1x}}{h},\frac{a_{1y}}{h},\frac{a_{1z}}{h} \right)$, $\left(\frac{a_{2x}}{k},\frac{a_{2y}}{k},\frac{a_{2z}}{k} \right)$, and $\left(\frac{a_{3x}}{l},\frac{a_{3y}}{l},\frac{a_{3z}}{l}\right)$. The normal vector to this plane can be determined by taking the cross product of two vectors in the plane. If $(h,k,l \ne 0)$, two suitable vectors are $\vec{v}_1=\frac{\vec{a}_1}{h}-\frac{\vec{a}_3}{l}$ and $\vec{v}_2=\frac{\vec{a}_2}{k}-\frac{\vec{a}_3}{l}$. The unit vector normal to the $(hkl)$ plane is called the pole of that crystallographic plane,
$$\hat{n}_{hkl}=\frac{\vec{v}_1\times \vec{v}_2}{|\vec{v}_1\times \vec{v}_2|}.$$The form below will calculate the translation vector for either the primitive unit cell or the conventional unit cell. With Miller indices, it is most common to use the conventional unit cell. For cubic crystals, $\vec{T}_{uvw}$ is normal to $(uvw)$ and parallel to $\hat{n}_{uvw}$ using the conventional unit cell, but this is not true for bcc or fcc using the primitive unt cell.
|
Rotatable image showing the $hkl$ plane in blue. $\vec{T}$ is the $[hkl]$ direction and $\hat{n}$ is the normal to the $hkl$ plane. |
A direction $[uvw]$ is in the $(hkl)$ plane if $\vec{T}_{uvw}\cdot\hat{n}_{hkl} = uh + vk + wl =0$. This is known as the Weiss zone law.
Since the position of every atom in a crystal is determined by the Bravais lattice and the basis of the crystal, it might be expected that crystallographers use these two quantities when they want to specify a crystal. However, what crystalographers typically specify is the space group and the asymmetric unit of the crystal. The space group is the collection of all symmetries, such as rotations and reflections, that the crystal has. The asymmetric unit is the minimum collection of atoms that are needed to reconstruct the basis by applying the symmetries of the space group to the asymmetric unit. If you operate on a crystal with one of the space group symmetries, the crystal looks the same before and after the symmetry operation. There is also a point group associated with every crystal structure, which is a subset of the space group. A point group is a collection of all symmetries where at least one point does not change during the symmetry operation. Point group symmetries such as reflections, rotations, and inversion can be represented as $3\times 3$ matrices. For instance, when the inversion matrix,
$$ \mathbf{i} = \left[\begin{matrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \\ \end{matrix}\right]$$operates on a vector, it leaves the point at the origin unchanged. A rotation such as
$$ \mathbf{C_4} = \left[\begin{matrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right]$$leaves all of the points on the $z-$axis unchanged. Another symmetry is an improper rotation, which involves a rotation and inversion. This is also called a rotoinversion.
$$ \mathbf{C_{4i}} = \left[\begin{matrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & -1 \\ \end{matrix}\right]$$A rotoinversion leaves the point at the origin unchanged. A reflection about the $x-y$ plane,
$$ \mathbf{\sigma_h} = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{matrix}\right]$$leaves all of the points in the $x-y$ plane unchanged.
In mathematics, a group is a set of elements where two of the elements can be combined in an operation to produce another element of that group. For example, the matrices,
$$ \mathbf{E} = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right], \qquad \mathbf{i} = \left[\begin{matrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \\ \end{matrix}\right]$$form a group. If you multiply these matrices with themselves or with each other, the result is always one of these two matrices. The matrix $\mathbf{E}$ is the identity matrix and is always an element of a group. Another group is
$$ \mathbf{E} = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right], \qquad \mathbf{C_4} = \left[\begin{matrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right], \qquad \mathbf{C_2} = \left[\begin{matrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right], \qquad \mathbf{C_4^3} = \left[\begin{matrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right].$$Here $\mathbf{E}$ is the identity element, $\mathbf{C_4}$ is a rotation of 90° around the $z-$axis, $\mathbf{C_2}$ is a rotation of 180° around the $z-$axis, and $\mathbf{C_4^3}$ is a rotation of 270° around the $z-$axis. Multiply any two matrices with themselves or with each other, and it will result in one of the matrices of this group.
There are 32 point groups, and every crystal can be assigned to a point group. This classification of crystals into point groups is important because the macroscopic properties of a crystal transform in a manner consistent with the symmetries of the point group. If you measure a property like the elastic constant, or the electrical conductivity, or the thermal conductivity, the property that is measured has to remain the same if you transform the crystal by a symmetry operation. Consider a rank 2 tensor (a matrix) property such as the electrical conductivity, which couples a vector electric field $\vec{E}$ to a vector current density $\vec{J}$,
$$ \vec{J}= \left[\begin{matrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \\ \end{matrix}\right]\vec{E}.$$If we now perform a matrix symmetry operation $\mathbf{U}$ on the vectors $\vec{J}$ and $\vec{E}$, then $\mathbf{U}\vec{J} = \mathbf{\sigma}\mathbf{U}\vec{E}$. Multiplying this by $\mathbf{U}^{-1}$ from the left results in the equation $\vec{J}= \mathbf{U}^{-1}\mathbf{\sigma}\mathbf{U}\vec{E}$. This means that for every symmetry operation $\mathbf{U}$ in the point group, the electrical conductivity matrix must satisfy $\mathbf{\sigma} = \mathbf{U}^{-1}\mathbf{\sigma}\mathbf{U}$.
As an example, consider the point group $m$, which consists of only the identity element and a reflection about the $x-y$ plane.
$$ \mathbf{E} = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right], \qquad \mathbf{\sigma_h} = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{matrix}\right].$$If $\mathbf{\sigma_h}$ is substituted for $\mathbf{U}$ in the equation $\mathbf{\sigma} = \mathbf{U}^{-1}\mathbf{\sigma}\mathbf{U}$ the result is,
$$\left[\begin{matrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \\ \end{matrix}\right] = \left[\begin{matrix} \sigma_{xx} & \sigma_{xy} & -\sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & -\sigma_{yz} \\ -\sigma_{zx} & -\sigma_{zy} & \sigma_{zz} \\ \end{matrix}\right].$$This can only be true if $\sigma_{xz}=\sigma_{yz}=\sigma_{zx}=\sigma_{zy}=0$ and the electrical conductivity matrix must have the form,
$$\mathbf{\sigma} = \left[\begin{matrix} \sigma_{xx} & \sigma_{xy} & 0 \\ \sigma_{yx} & \sigma_{yy} & 0 \\ 0 & 0 & \sigma_{zz} \\ \end{matrix}\right].$$This must hold for any of the millions of crystals that have point group $m$ and for any property that is described by a matrix, such as the electrical conductivity, the thermal conductivity, electric susceptibility, magnetic susceptibility, thermal expansion, Peltier effect (heat current due to electrical current), Seebeck effect (Electric field due to thermal gradient), etc.
To better understand the tensor properties of solids, consider the strain matrix. If we draw coordinate axes $x$, $y$, and $z$ on a crystal and then deform the crystal, the coordinate axes change their length and direction to $x'$, $y'$, and $z'$. The relation of the axes before and after deformation can be described by the strain matrix,
$$\left[\begin{matrix} x' \\ y' \\ z' \end{matrix}\right] = \left[\begin{matrix} 1 + \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{yx} & 1+\epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{zx} & \epsilon_{zy} & 1+\epsilon_{zz} \\ \end{matrix}\right]\left[\begin{matrix} x \\ y \\ z \end{matrix}\right].$$The strain is related to properties such as piezoelectricity. If the atoms in the crystal transfer some charge when they bond, some of the atoms will be more positively charged and some will be more negatively charged. This can result in a net polarization of the unit cell. If a strain can move the atoms in such a way that it changes the polarization, the material is called piezoelectric. This is used, for instance, to light a gas grill. By compressing a piezoelectric crystal, the change in polarization causes a voltage across a small gap, which sparks to light the gas.
We can write the relation between polarization and strain using Einstein notation,
$$P_i = d_{ijk}\epsilon_{jk}.$$Here $d_{ijk}$ is the piezoelectric tensor. In Einstein notation, each of the indices $i$, $j$, and $k$ can take the values $x$, $y$, and $z$. If the indices are repeated on one side of an equation, you sum over the repeated indices. Since $j$ and $k$ both repeat on the right side of the equation, this is equivalent to,
$$P_x = d_{xxx}\epsilon_{xx} + d_{xxy}\epsilon_{xy} + d_{xxz}\epsilon_{xz} + d_{xyx}\epsilon_{yx} + d_{xyy}\epsilon_{yy} + d_{xyz}\epsilon_{yz} + d_{xzx}\epsilon_{zx} + d_{xzy}\epsilon_{zy} + d_{xzz}\epsilon_{zz}, \\ P_y = d_{yxx}\epsilon_{xx} + d_{yxy}\epsilon_{xy} + d_{yxz}\epsilon_{xz} + d_{yyx}\epsilon_{yx} + d_{yyy}\epsilon_{yy} + d_{yyz}\epsilon_{yz} + d_{yzx}\epsilon_{zx} + d_{yzy}\epsilon_{zy} + d_{yzz}\epsilon_{zz}, \\ P_z = d_{zxx}\epsilon_{xx} + d_{zxy}\epsilon_{xy} + d_{zxz}\epsilon_{xz} + d_{zyx}\epsilon_{yx} + d_{zyy}\epsilon_{yy} + d_{zyz}\epsilon_{yz} + d_{zzx}\epsilon_{zx} + d_{zzy}\epsilon_{zy} + d_{zzz}\epsilon_{zz}.$$Einstein notation is much more compact than writing the equations out fully. The 27 reciprocal piezoelectric coefficients $d_{ijk}$ form a rank 3 tensor. The rank of a tensor is the number of indices.
In the reciprocal piezoelectric effect, an electric field acts on the charged atoms in a crystal, pushing the positively charged atoms in one direction and the negatively charged atoms in the opposite direction. This can distort the shape of the crystal and this distortion is described by a strain matrix. In Einstein notation, this would be,
$$\epsilon_{ij} = g_{ijk}E_k.$$Since there are 9 possible combinations of $i$ and $j$ and $k$ repeats on the right side, this is 9 equations, each with 3 terms.
An example of a fourth rank tensor is the piezoconductivity tensor $\beta$. It describes how the electrical conductivity of a material changes when it is strained. In Einstein notation, this would be written, $$\sigma_{ij} = \beta_{ijkl}\epsilon_{kl}.$$
This is 9 equations each with 9 terms on the right side. Piezoconductive silicon is often used to construct the accelerometer in a mobile phone. The acceleration deforms a silicon cantilever and the change in conductivity is detected electrically.
Generally, any property of a solid can be written as a tensor. It can be a scalar property like the density (a rank 0 tensor), or a vector property like the electric polarization (a rank 1 tensor), or a matrix property like the electrical conductivity (a rank 2 tensor), or a rank 3 tensor like the piezoelectric effect, or a rank 4 tensor like the piezoconductivity, etc. We will not go into the mathematics of transforming the higher rank tensors by symmetry operations. However, all properties of solids are some kind of tensor and the tensors are restricted by the point group of the crystal. There is a table of the 32 point groups that lists all of the symmetry elements of each point group and gives the form of the rank 1, rank 2, rank 3, and rank 4 tensors. The table distinguishes between symmetric tensors and asymmetric tensors. Sometimes the physics of a property, requires tensor elements to be symmetric ($M_{ij} = M_{ji}$).
There are a few notable consequences of symmetry. Eleven of the thirty-two point groups contain inversion. If there is inversion in the group, all odd-ranked tensor properties of those crystals are zero. This means that crystals with inversion in their point group cannot be piezoelectric or exhibit the nonlinear optical property of second harmonic generation. Another interesting consequence of symmetry is that all rank 2 tensors of cubic crystals are diagonal matrices where the three diagonal elements are all the same. Many common crystals are cubic, such as silver, gold, copper, iron, silicon, germanium, diamond, and GaAs. The rank 2 tensor properties of these cubic crystals, such as the electrical conductivity or thermal conductivity, are typically specified by a single scalar instead of a matrix because only one number needs to be given to specify the whole matrix.
Knowing the point group of a crystal is important to know the forms of the tensor properties, but the point group does not uniquely specify the Bravais lattice of a crystal. This is why crystallographers typically classify crystals by their space group. The space group uniquely determines the point group and the Bravais lattice as shown in this table: Space Group → Bravais Lattice, Point Group. A space group includes the symmetry operations of the point groups (reflection, rotation, and inversion), plus screw axis symmetries and glide plane symmetries. In a screw axis symmetry, the crystal needs to be rotated and translated before it maps onto itself. For a glide plane symmetry, the crystal must be reflected and translated before it maps onto itself. The screw axis symmetries and glide plane symmetries are also necessary for constructing the basis from the asymmetric unit. The standard reference, which describes the 230 space groups is the International Tables for Crystallography. This is a 10-volume set that requires a subscription. Volume D discusses the relationship between the tensor properties of crystals and their symmetries.
Each of the 14 Bravais lattices has a different space group symmetry. However, some of the Bravais lattices share a point group. The 7 crystal systems correspond to the 7 point groups of the Bravais lattices. The space groups and point groups of the Bravais lattices are listed in this table.
|
|
|
|
Historically, crystal structures were labeled using a Strukturbericht designation. This specifies both the space group and the basis. In the Strukturbericht classification, crystal structures are assigned to a symbol that is a combination of letters and numbers. The crystal structures of type $A$ consist of only one element. For instance, an fcc crystal with one atom in the basis is $A1$, and a bcc crystal with one atom in the basis is $A2$. Crystal structures of type $B$ contain 2 elements in a 1:1 ratio. Crystal structures of type $C$ contain 2 elements in a 1:2 ratio. Crystal structures of type $D$ contain 2 elements in a general $n:m$ ratio. Types E through S describe more complex compounds. A good reference for the Strukturbericht classification is the Encyclopedia of Crytallographic Prototypes.
Although there are only 14 Bravais lattices, there are hundreds of thousands of known crystal structures. In this section, 10 common crystal structures are described.
The only element that forms a simple cubic crystal structure is polonium.
| $\vec{a}_1 = a\hat{x}\\ \vec{a}_2 = a\hat{y}\\ \vec{a}_3 = a\hat{z}$ | 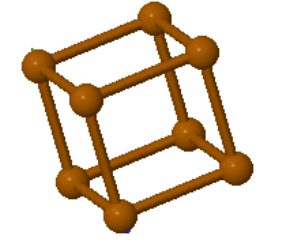 α-Polonium |
| $a$ is the length of a side of the cube. | |
Space group: $Pm\overline{3}m$ #221
Point group: $m3m = O_h$
Bravais lattice: Simple Cubic
Strukturbericht: Ah
Pearson symbol: cP1
Prototype: α-Po
Asymmetric unit: Po (0,0,0)
Basis: Po (0,0,0)
Every atom has 6 nearest neighbors.
The positions of the atoms in the asymmetric unit and the basis are given in fractional coordinates $(m,n,l)$ where $0 \le m,n,l \le 1$ and the position of the atom is $m\vec{a}_1 + n\vec{a}_2 + l\vec{a}_3$ using the lattice vectors of the primitive unit cell. The number of nearest neighbors is also called the coordination number.
 |  |  | ||
 |  |  | ||
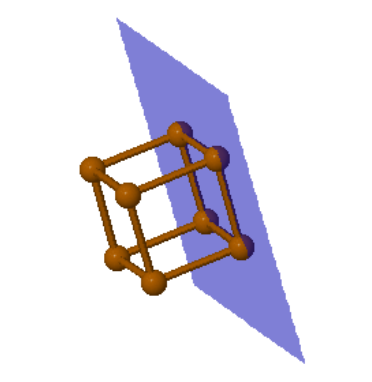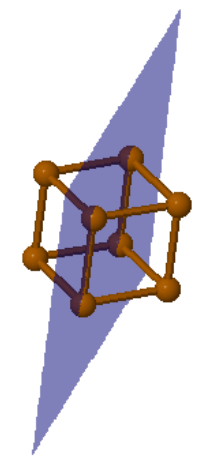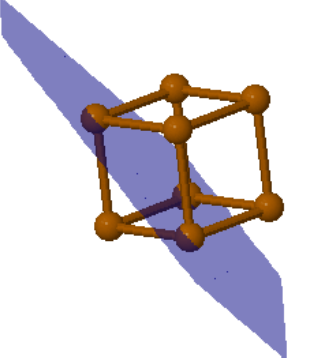Po (100) | Po (110) | Po (111) |
Many elemental metals (Li, Na, K, V, Cr, Fe, Rb, Nb, Mo, Cs, Ba, Eu, Ta, W) form the bcc crystal structure.
| $\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{y}-\hat{z})\\ \vec{a}_2=\frac{a}{2}(-\hat{x}+\hat{y}+\hat{z})\\ \vec{a}_3=\frac{a}{2}(\hat{x}-\hat{y}+\hat{z})$ | 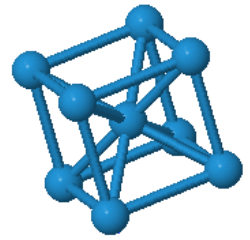 Tungsten |
| $a$ is the length of a side of the cube. | |
Space group: $Im\overline{3}m$ #229
Point group: $m3m = O_h$
Bravais lattice: Body-Centered Cubic
Strukturbericht: A2
Pearson symbol: cI2
Prototype: W
Asymmetric unit: W (0,0,0)
Basis of the primitive unit cell: W (0,0,0)
Basis of the conventional unit cell: W (0,0,0), W (½,½,½)
Every atom has 8 nearest neighbors.
 |  |  | ||
 |  |  | ||
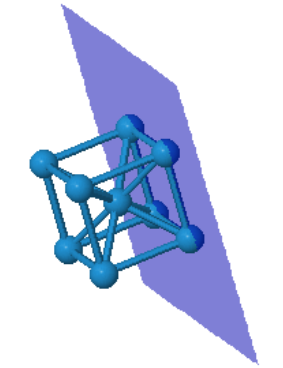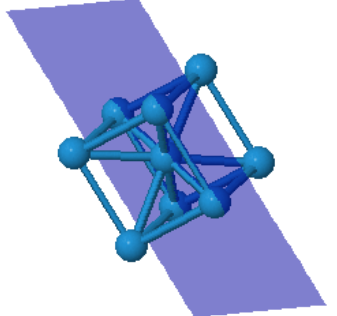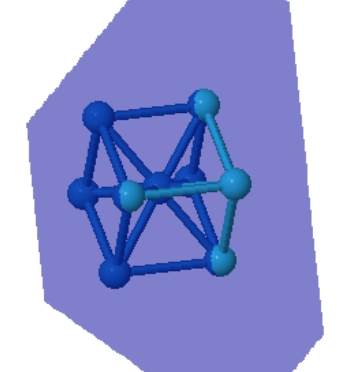W (100) | W (110) | W (111) |
Fcc is one of the close-packed structures where every atom has 12 equivalent nearest neighbors. The close-packed planes are the {111} planes. Many elemental metals (Al, Ag, Au, Ce, Cu, Ir, Ni, Pb, Pd, Pt, Rh, Sr, Tb, Th) form the fcc crystal structure.
| $\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z})\\ \vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y})\\ \vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z})$ | 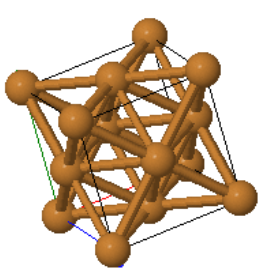 Copper |
| $a$ is the length of a side of the cube. | |
Space group: $Fm\overline{3}m$ #225
Point group: $m3m = O_h$
Bravais lattice: Face-Centered Cubic
Strukturbericht: A1
Pearson symbol: cF4
Prototype: Cu
Asymmetric unit: Cu (0,0,0)
Basis of the primitive unit cell: Cu (0,0,0)
Basis of the conventional unit cell: Cu (0,0,0), Cu (½,½,0), Cu (½,0,½), Cu (0,½,½)
Every atom has 12 nearest neighbors.
 |  |  | ||
 |  |  | ||
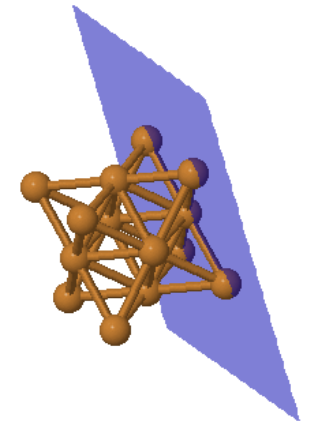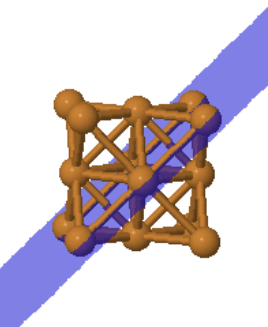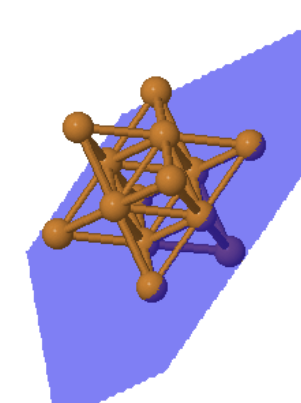| Cu (100) | Cu (110) | Cu (111) |
The (111) plane of fcc is a close-packed plane. Every atom has 6 nearest neighbors. This is the closest packing of spheres that can be achieved in two dimensions. There are two positions to put another close-packed layer on top of this layer, B and C.
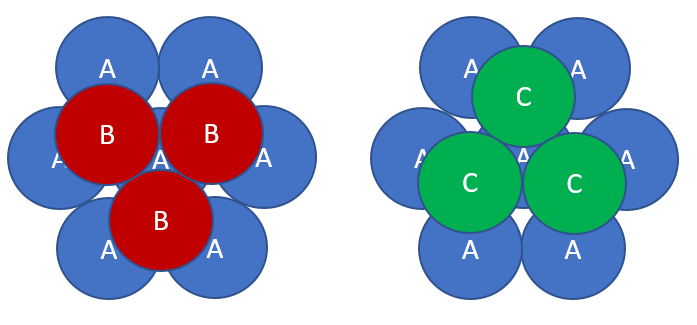
In the fcc crystal structure, the two-dimensional close-packed layers are stacked ABCABC$\cdots$ perpendicular to the [111] direction.
Hcp is also a close-packed structure where every atom has 12 equivalent nearest neighbors. The close-packed planes are the {001} planes with a stacking ABAB$\cdots$. Many elemental metals (Mg, Ti, Co, Be, Sc, Y, Zr, Tc, Ru, Cd, Hf, Re, Os, Tl) form the hcp crystal structure.
| $\vec{a}_1=\frac{a}{2}\hat{x}-\frac{\sqrt{3}a}{2}\hat{y}\\ \vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y}\\ \vec{a}_3=c\hat{z}$ | 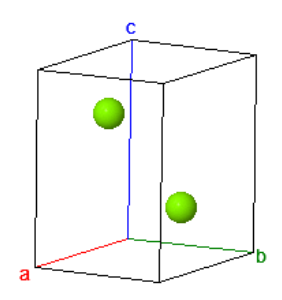 Magnesium | 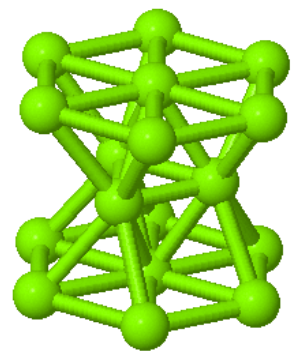 Hexagonal unit cell |
| $a$ is the length of a side of a triangle in the close packed plane. $c$ is the distance between the close-packed planes. | ||
Space group: $P6_3/mmc$ #194
Point group: $\frac{6}{m}mm = D_{6h}$
Bravais lattice: Hexagonal
Strukturbericht: A3
Pearson symbol: hP2
Prototype: Mg
Asymmetric unit: Mg (⅓,⅔,¼)
Basis: Mg (⅓,⅔,¼), Mg (⅔,⅓,¾)
Every atom has 12 nearest neighbors.
The diamond crystal structure is formed by carbon, silicon, germanium, and tin at low temperatures. The Bravais lattice is fcc, and there are two atoms in the basis.
| $\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z})\\ \vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y})\\ \vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z})$ | 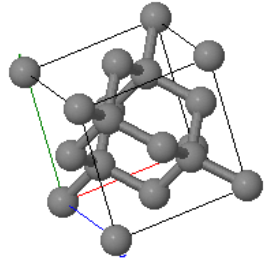 Diamond |
| $a$ is the length of a side of the cube. | |
Space group: $Fd\overline{3}m$ #227
Point group: $m3m = O_{h}$
Bravais lattice: Face-centered cubic
Strukturbericht: A4
Pearson symbol: cF8
Prototype: C
Asymmetric unit: C (0,0,0)
Basis: C (0,0,0), C (¼,¼,¼)
Every atom has 4 nearest neighbors.
The cesium chloride (CsCl) structure has a simple cubic Bravais lattice and two atoms in the basis. This is one of the crystal structures associated with ionic crystals. Ionic crystals consist of positively charged atoms and negatively charged atoms. The nearest neighbors of the positively charged atoms are negatively charged, while the nearest neighbors of the negatively charged atoms are positively charged. If a crystal is constructed from equally sized positively charged spheres and negatively charged spheres, and only the Coulomb forces are considered, the crystal structure with the lowest energy is the CsCl structure. In this crystal structure, each atom has 8 nearest neighbors of the opposite charge.
| $\vec{a}_1 = a\hat{x}\\ \vec{a}_2 = a\hat{y}\\ \vec{a}_3 = a\hat{z}$ |
|
|
| $a$ is the length of a side of the cube. | ||
To calculate the Coulomb energy, we notice that each atoms has
If we assume that a charge of one electron is transferred from the Cs atom to the Cl atom, then the change in potential energy per atom that results from bringing these charged ions together from far apart is,
$$U = -\frac{e^2}{4\pi\epsilon R} \left(8 - 6\frac{2}{\sqrt{3}}+12\frac{2\sqrt{2}}{\sqrt{3}} - 8\cdot 2 + \cdots\right),$$where $R = \frac{\sqrt{3}a}{2}$ is the distance between nearest neighbors. The sum of the series in round brackets is called the Madelung constant $\alpha$. For CsCl, $\alpha = 1.763$.
Space group: $Pm\overline{3}m$ #221
Point group: $m3m = O_{h}$
Bravais lattice: Simple cubic
Strukturbericht: B2
Pearson symbol: cP2
Prototype: CsCl
Asymmetric unit: Cs (0,0,0), Cl (½,½,½)
Basis: Cs (0,0,0), Cl (½,½,½)
Every atom has 8 nearest neighbors.
Other crystals that form the CsCl crystal structure are: AgCd, AgCe, AgDy, AgGd, AgHo, AgLa, AgLi, AgLu, AgMg, AgNd, AgSc, AgSm, AgTb, AgTm, AgZn, AlCe, AlCo, AlDy, AlFe, AlIr, AlLu, AlMg, AlNd, AlNi, AlOs, AlPd (H.T.), AlRe, AlRh, AlRu, AuCd, AuCs, AuDy, AuGd, AuHRb, AuHo, AuLa, AuLi, AuLu, AuMg, AuMn (H.T.), AuNd, AuPr, AuSc, AuSm, AuTb, AuTi (H.T.), AuTm, AuY, AuZn, BaCd, BaHg, BeNi, BePd, BiTl, CaCd, CaHg, CaIn, CaTl, CdCe, CdGd, CdLa, CdPr, CdSc, CdSm, CdSr, CdY, CeHg, CeMg, CeZn, CoFe, CoGa, CoHf, CoSc, CoTi, CoZr, CuDy, CuEr, CuGd, CuSc, CuSm, CuTb, CuTm, CuY, DyIn, DyMg, DyTl, DyZn, ErMg, ErZn, FeRh, FeTi, FeV, GaIr, GaNi, GaRu, GdHg, GdIn, GdMg, GdRh, GdTl, GdZn, HfRu, HfTc, HgLa, HgLi, HgMg, HgMn, HgPr, HgSc, HgSr, HgY, HoIr, HoMg, HoRh, HoZn, InNi, InPd, IrMn, IrSc, IrTm, LuMg, LuPd, LuRh, MgNd, MgPd, MgPr, MgRh, MgSm, MgTb, MgTm, MgV, NdTl, NdZn, NiSc, NiTi, NiZn (H.T.), OsTl, OsV, OsZr, PdSc, PdSm, PdZn, PtSc, PuRu, ReTi, RhSc, RhSi, RhSm, RhTb, RhTi, RhTm, RhZr, ScZn, SmZn, SrTl, TaTc, TbZn, TcTi, TcV, TeTh, TiZn, TlY, TmZn, YZn
The NaCl crystal structure has an fcc Bravais lattice with two atoms in the asymmetric unit and two atoms in the basis.
| $\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z})\\ \vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y})\\ \vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z})$ |
|
|
| $a$ is the length of a side of the cube. | ||
NaCl is another common crystal structure for ionic crystals. The Coulomb energy is calculated with the sum,
$$U = -\frac{e^2}{4\pi\epsilon R} \left(6 - \frac{12}{2}+\frac{8}{3} - \frac{6}{4} + \frac{24}{5} +\cdots\right)= -\frac{\alpha e^2}{4\pi\epsilon R} ,$$where in this case $\alpha = 1.747$. The reduction in Coulomb energy is less for NaCl than it is for CsCl. This is related to the fact that each atom of CsCl has 8 nearest neighbors while in NaCl each atom has 6 nearest neighbors.
Space group: $Fm\overline{3}m$ #225
Point group: $m3m = O_{h}$
Bravais lattice: Face-centered cubic
Strukturbericht: B1
Pearson symbol: cF8
Prototype: NaCl
Asymmetric unit: Na (0,0,0), Cl (½,½,½)
Basis of the primitive unit cell: Na (0,0,0), Cl (½,½,½)
Every atom has 6 nearest neighbors.
Other crystals that form the NaCl crystal structure are: AgCl, AmO, BaO, BaPo, BaS, BaSe, BaTe, CaO, CaPo, CaS, CaSe, CdO, CeAs, CeBi, CeN, CeP, CeS, CeSb, CeSe, CeTe, CoO, CrN, DyAs, DyBi, DyN, DyP, DyS, DySb, DySe, DyTe, ErAs, ErBi, ErN, ErP, ErS, ErSb, ErSe, ErTe, EuN, EuO, EuS, EuSe, EuTe, GdAs, GdN, GdSb, GdSe, GdTe, HfB, HfC, HfN, HoAs, HoBi, HoN, HoP, HoS, HoSb, HoSe, HoTe, KBr, LaAs, LaBi, LaN, LaP, LaS, LaSb, LaTe, LiCl, LiF, LiH, LuN, LuS, LuSb, MgO, MgS, MgSe, MnO, MnS, MnSe, MnTe, NU, NaBr, NaF, NaH, NbO, NdAs, NdBi, NdN, NdP, NdS, NdTe, NiO, NpC, NpN, NpO, PaO, PbPo, PbS, PbSe, PbTe, PdH, PrAs, PrBi, PrN, PrP, PrS, PrSb, PrSe, PuAs, PuB, PuBi, PuC, PuN, PuO, PuP, PuS, PuTe, RbF, RbH, ScAs, ScBi, ScC, ScN, ScP, ScSb, SmAs, SmN, SmO, SmP, SmS, SmSe, SmTe, SmTm, SnAs, SnSb, SnSe, SrO, SrS, SrTe, TaC, TaO, TbAs, TbBi, TbN, TbP, TbS, TbSb, TbSe, TbTe, ThAs, ThC, ThGe, ThN, ThSb, TiC, Tin, TiO, TmAs, TmBi, TmN, TmP, TmSb, TmSe, TmTe, UAs, UBi, UC, UO, UP, US, USb, USe, UTe, VO, YAs, YBi, YN, YP, YS, YSb, YSe, YTe, YbAs, YbN, YbO, YbP, YbS, YbSb, YbSe, YbTe, ZnSe, ZrB, ZrC, ZrN, ZrO, ZrS
Zincblende is a cubic crystal structure that is similar to diamond. The basis consists of one Zn atom at (0,0,0) and one S atom at (¼,¼,¼). These two atoms are repeated on an fcc Bravais lattice to form the crystal structure. If all of the atoms were of the same type, it would be the diamond crystal structure. Many semiconductors such as GaAs, InAs, GaP, GaSb, HgTe, InP, and InSb form the zincblende structure. Often, the bonds between the atoms are partly ionic, and there is some charge transfer between the atoms. The Madelung constant for zincblende is $\alpha = 1.638$
| $\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z})\\ \vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y})\\ \vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z})$ | 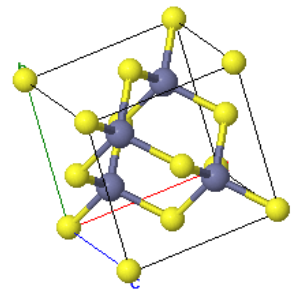 Zincblende |
| $a$ is the length of a side of the cube. | |
Space group: $F\overline{4}3m$ #216
Point group: $\overline{4}3m = T_{d}$
Bravais lattice: Face-centered cubic (cF)
Strukturbericht: B3
Pearson symbol: cF8
Prototype: ZnAs
Asymmetric unit: Zn (0,0,0), As (¼,¼,¼)
Basis: Zn (0,0,0), As (¼,¼,¼)
Every atom has 4 nearest neighbors.
Other crystals that form the zincblende crystal structure are: AgI, AlAs, AlP, AlSb, AsB, AsGa, AsIn, BN, BePo, BeS, BeSe, BeTe, β-CsSi, CdPo, CdS, CdSe, CdTe, CuI (marshite), FeN, GaP, GaSb, HgS, HgSe, HgTe, InP, InSb, β-MnS, β-MnSe, OZn, PoZn, SSn, SZn, TeZn
Wurtzite is a hexagonal crystal structure with two atoms in the asymmetric unit and four atoms in the basis. It is related to the hexagonal diamond structure. Many semiconductors that form the wurtzite structure are semiconductors. Often, the bonds between the atoms are partly ionic, and there is some charge transfer between the atoms. The Madelung constant of wurtzite is $\alpha = 1.641$.
|
|
|
|
Space group: $P6_3mc$ #186
Point group: $6mm = C_{6v}$
Bravais lattice: Hexagonal
Strukturbericht: B4
Pearson symbol: hP4
Prototype: ZnS
Asymmetric unit: Zn1 (⅓,⅔,0), S1 (⅓,⅔,$z_1$)
Basis: Zn1 (⅓,⅔,0), S1 (⅓,⅔,$z_1$) Zn2 (⅔,⅓,½), S2 (⅔,⅓,$z_1+\frac{1}{2}$)
Every atom has 4 nearest neighbors.
Here $z_1 = 0.3748$ for ZnS but can differ for other compounds with this crystal structure. Other crystals that form the wurtzite crystal structure are: β-AgI, AlN, BN, BeO, CdS, CdSe, CdSe, CuH, β-CuI, GaN, InN, MgTe, γ-MnS, γ-MnSe, SiC, ZnO, ZnSe
Perovskite is a crystal structure with a simple cubic Bravais lattice and five atoms in the basis. The cubic form is typically the high-temperature phase of perovskite compounds. They often go through a structural phase transition to a tetragonal phase or some other phase with lower symmetry. Perovskites are often ferroelectrics, piezoelectrics, and pyroelectrics. They can have very high dielectric constants and are used in supercapacitors. There are perovskite superconductors, and they have promising applications in solar cells.
| $\vec{a}_1 = a\hat{x}\\ \vec{a}_2 = a\hat{y}\\ \vec{a}_3 = a\hat{z}$ | ||
| $a$ is the length of a side of the cube. | ||
Space group: $Pm\overline{3}m$ #221
Point group: $m3m = O_{h}$
Bravais lattice: Simple Cubic
Strukturbericht: E21
Pearson symbol: cP5
Prototype: CaTiO3
Asymmetric unit: Ti (0,0,0), Ca (0.5,0.5,0.5), O (0.5,0.5,0)
Basis: Ti (0,0,0), Ca (0.5,0.5,0.5), O (0.5,0.5,0), O (0.5,0,0.5), O (0,0.5,0.5)
Other crystals that form the perovskite crystal structure are: AlCFe3, AlCMn3, AlCTi3, AlNMn3, AuOCs3, BaCeO3, BaCrO3, BaLiH3, BaPuO3, BaSnO3, BaTiO3, BaZrO3, BiFeO3, CeCRu3, CeCrO3, CuNMn3, EuTiO3, GaCMn3, GaNMn3, GeCMn3, InCTi3, InNTi3, KMgF3, KTaO3, LaAlO3, LaGaO3, MgCNi3, MgNaF3, NiNFe3, NiNMn3, PbTiO3, PbZrO3, PdNFe3, PrCoO3, PtNFe3, RbFeF3, SmCoO3, SmCrO3, SnCFe3, SnNFe3, SrLiH3, SrRuO3, SrTiO3, SrTlO3, TlCTi3, TlNTi3, YAlO3, ZnCMn3, Ba3N2, Ba3P2, Ba3Sb2
Polymorphism is when crystals with the same chemical composition have different crystal structures. A striking example is carbon, which can form in the diamond crystal structure or the graphite crystal structure. Both crystals are made exclusively of carbon atoms, but when the atoms are arranged in the diamond structure, they form a hard, transparent, electrically insulating material, while when the same type of atoms are arranged in the graphite structure, the form a soft, black, electrical conductor.
|
|
There are more than 250 known polytypes of SiC. Four of the most common polytypes are shown below. The properties of SiC depend on which polytype is formed.
|
|
|
|
Polymorphism is very common. Almost any compound will form more than one crystal structure. At a given temperature and pressure, usually one structure is thermodynamically stable, but other crystal structures may be metastable under those conditions. For instance, graphite is the thermodynamically stable phase of carbon at room temperature and ambient pressure. Diamond is metastable under these conditions. However, it would take a large amout of energy to break the bonds in diamond to be able to rearrange the atoms into graphite. This energy barrier makes diamond seem stable in practice. When the atoms of a compound rearrange from one crystal structure to another, this is called a structural phase transition.
There are databases with hundreds of thousands of crystal structures. Some open databases are:
The first two are filled with experimental data while the Materials Project calculates crystal structures from first principles. Important crystal databases that require a subscription are:
These databases typically have search functions to help you find a crystal based on its chemical composition. Crystal structure data is usually stored in a Crystallographic Information File (a CIF file). This is a text file that contains the space group, the lattice parameters ($a$, $b$, $c$, $\alpha$, $\beta$, $\gamma$), the asymmetric unit of the crystal, and a reference to where the data was first published. It is important to check the publication to see the conditions used during the experiment because the distances between the atoms in a crystal depend on the temperature and the pressure. Below are some links to some example crystal structures and their corresponding CIF files.
Below is a period table of the elements with links to their common crystal structures. Many elements undergo structural phase transitions from one crystal structure to another under changing conditions of temperature and pressure. The crystal structures formed by the elements are shown in the list of Strukturbericht type A crystal structures.
1 |
2 | ||||||||||||||||
3 |
4 |
5 |
7 |
8 |
9 |
10 |
|||||||||||
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
||||||||||
19 |
21 |
23 |
24 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
||||
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
51 |
52 |
53 |
54 |
|
55 |
56 |
57 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
104 |
105 |
106 |
107 |
108 |
109 |
|||||||||
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
sc = Simple Cubic, fcc = Face-centered Cubic, bcc = Body-centered Cubic, hex = Hexagonal, rho = Rhombohedral
tP = Simple Tetragonal, tI = Body-centered Tetragonal
oP = Simple Orthorhomic, oS = Base-centered Orthorhomic, oF = Face-centered Orthorhomic, oI = Body-centered Orthorhomic
mP = Simple Monoclinic, mS = Base-Centered Monoclinic, tri = Triclinic
If you search the internet for a crystal name such as 'rutile' and 'cif', you will probably be able to download the cif file for that crystal. There are freely available programs that can read CIF files and draw the crystals. Two of these programs are Mercury and PowderCell.
Another possibility is to open the CIF file in an online tool like JSmol, which is embedded in the frame below.
To load a cif file that you have downloaded, right-click on the background of the image of the crystal and choose 'File' → 'Load' → 'Open local file'.
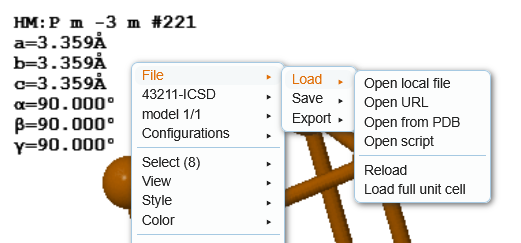
This should bring up a gray bar with a 'Browse...' button. Press the 'Browse...' button and find the cif file you want to load. Then press the 'load' button.
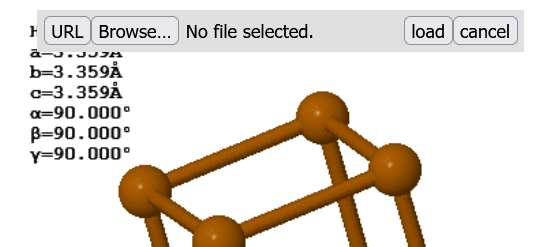
To find the distance between atom A and atom B in JSmol, double-click on atom A, then double-click on atom B. To find the angle formed by atoms A, B, and C, double-click on atom A, single-click on atom B, and double-click on atom C. JSmol can also be used to view how the atoms are arranged in the $(hkl)$ planes.
In the Encyclopedia of crystallographic prototypes, if you choose a crystal structure and scroll to the bottom of the page, you will find a button that will generate a CIF file for that crystal structure. There are also buttons for generating input for programs that calculate the electronic structure of crystals such as VASP, Quantum Espresso, FHI-AIMS, ABINIT, and ELK. These codes are used to calculate the electronic, magnetic, optical, mechanical, and thermodynamic properties of materials based on the arrangement of the atoms in the crystal.
